|
Question 1205325: Simplify the following:

Found 3 solutions by ikleyn, math_tutor2020, Edwin McCravy:
Answer by ikleyn(52915)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor @ikleyn probably has the most efficient pathway, but here's another approach.
The pattern in the numerator (1^2,3^2,5^2,7^2,...) follows the sequence (2k-1)^2 where k is an integer and k = 1 is the starting index.
Note how 1,3,5,7,... is an arithmetic sequence.
The highest that k goes is k = 52 because 2k-1 = 2*52 - 1 = 103.
The pattern in the denominator (2,6,10,14,...) is also arithmetic and follows the sequence 4k-2
Note that 4k-2 = 4*52 - 2 = 206.
Each term can be written of the form 
We're tasked to find the summation 
Use these summation identities

and

and

to have the following steps



Therefore,

Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
You can put this solution on YOUR website!
How about this way?:
 0.5 + 1.5 + 2.5 + 3.5 + ... + 51.5 =
The sum of the whole parts:
0 + 1 + 2 + 3 + ... + 51 =
0.5 + 1.5 + 2.5 + 3.5 + ... + 51.5 =
The sum of the whole parts:
0 + 1 + 2 + 3 + ... + 51 = 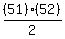 = 1326
PLUS
the sum of the 52 decimal parts of 0.5 each:
52 x 0.5 = 26
EQUALS
1352
Edwin = 1326
PLUS
the sum of the 52 decimal parts of 0.5 each:
52 x 0.5 = 26
EQUALS
1352
Edwin
|
|
|
| |