|
Question 1205247: 1.Find the equation of the circle that passes through the points (0,0), (5,0), and (3,3). Use both geometric and algebraic solution for comparison.
2. The cable of a suspension bridge hangs in the shape of a parabola. The tower supporting the cable are 400 ft apart and 150 ft high. If the cable, at its lowest, is 30 ft above the bridge at its midpoint, how high is the cable 50 ft away(horizontally) from either tower?
Found 3 solutions by ikleyn, Edwin McCravy, greenestamps:
Answer by ikleyn(52824)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
2. The cable of a suspension bridge hangs in the shape of a parabola.
The tower supporting the cable are 400 ft apart and 150 ft high.
If the cable, at its lowest, is 30 ft above the bridge at its midpoint,
how high is the cable 50 ft away(horizontally) from either tower?
~~~~~~~~~~~~~~~~~~~~~~~~
Place the origin of the coordinate system half way between the towers,
at the level of the bridge.
Using vertex form, write equation of a parabola
y = ax^2 + 30.
Find the unknown coefficient "a" from the condition
a*200^2 + 30 = 150 ft,
which says that the cable is suspended at the top of a tower (for each cable and each tower).
From this equation, find "a"
40000a = 150 - 30 = 120
a =  = = 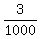 = 0.003.
So, the parabola equation is
y = 0.003*x^2 + 30.
They want you find "y" at x = 200-50 = 150 ft.
Substitute x= 150 into equation of the parabola and get
y = 0.003*150^2+30 = 97.5 ft.
ANSWER. 50 ft away from either tower, the cable is 97.5 ft over the bridge. = 0.003.
So, the parabola equation is
y = 0.003*x^2 + 30.
They want you find "y" at x = 200-50 = 150 ft.
Substitute x= 150 into equation of the parabola and get
y = 0.003*150^2+30 = 97.5 ft.
ANSWER. 50 ft away from either tower, the cable is 97.5 ft over the bridge.
Solved.
//////////////////
NEVER pack more than 1 (one) problem per post.
It is against the rules of this forum; against the common sense,
perpendicular to the rules of good behavior and against your own interests.
For the rules of this forum, read at this web-page
https://www.algebra.com/tutors/students/ask.mpl?action=ask_question&topic=Equations&return_url=http://www.algebra.com/algebra/homework/equations/
from which you post your problems. Read it attentively and find there many useful instructions.
Become a civilized user / visitor . . .
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Ikleyn did the parabola problem for you. I'll do the circle problem. 1.Find the equation of the circle that passes through the points (0,0), (5,0),
and (3,3). Use both geometric and algebraic solution for comparison.OK, I'll try to show the straight-edge and compass geometric method to draw
a circle through three points.
 The geometric method is to find the center by:
1. drawing two chords,
The geometric method is to find the center by:
1. drawing two chords,
 2. drawing their perpendicular bisectors (in green):
2. drawing their perpendicular bisectors (in green):
 3. the center is where those two perpendicular bisectors of 2 chords intersect.
(it looks like the point
3. the center is where those two perpendicular bisectors of 2 chords intersect.
(it looks like the point 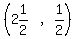 , but we aren't sure
of it being exactly that with the geometric method.)
4. Put the foot of the compass on the point where the perpendicular bisectors
of the two chords intersect. The open your compass to one of the points on
the circle. Then swing it around and draw a circle. , but we aren't sure
of it being exactly that with the geometric method.)
4. Put the foot of the compass on the point where the perpendicular bisectors
of the two chords intersect. The open your compass to one of the points on
the circle. Then swing it around and draw a circle.
 That's the geometric way to draw a circle through three points.
But the algebraic way is to begin with the general equation
or the standard equation for a circle:'
It might be easier to substitute the three points in the standard equation:
That's the geometric way to draw a circle through three points.
But the algebraic way is to begin with the general equation
or the standard equation for a circle:'
It might be easier to substitute the three points in the standard equation:


 Subtract the 1st equation from the other two equations:
Subtract the 1st equation from the other two equations:


 Solve the 2nd equation for h
Solve the 2nd equation for h
 Substitute 5/2 for h in the 3rd equation
Substitute 5/2 for h in the 3rd equation
 Multiply the 3rd equation by 2
Multiply the 3rd equation by 2



 Substitute h=5/2, k=1/2 in the 1st equation:
Substitute h=5/2, k=1/2 in the 1st equation:



 So the standard form is
So the standard form is

 So now we see that the center = (h,k) =
So now we see that the center = (h,k) =  and the radius is
and the radius is 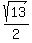 So we graph the circle
So we graph the circle
 Other times we might just want the general equation
Other times we might just want the general equation
 Substitute the three points in:
Substitute the three points in:


 Substitute c=0 in the other two equations:
Substitute c=0 in the other two equations:
 Divide the 2nd equation by 5 and the third by 3
Divide the 2nd equation by 5 and the third by 3
 Solve the 2nd equation for 'a'
Solve the 2nd equation for 'a'
 Substitute a = -5 in the third equation:
Substitute a = -5 in the third equation:
 Solve the 3rd equation for b
Solve the 3rd equation for b
 Substitute in the general solution:
Substitute in the general solution:


 But the trouble with the general equation of a circle is that we can't tell
the center and radius from it unless we complete the square and get it into
the standard form.
The general form
But the trouble with the general equation of a circle is that we can't tell
the center and radius from it unless we complete the square and get it into
the standard form.
The general form  and the standard form and the standard form  are equivalent.
Edwin
are equivalent.
Edwin
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I don't know what it means to use a geometric solution to find the equation of a circle. At some point, no matter how much work you do with geometry, you need to use algebra to get an equation.
The perpendicular bisector of any chord of a circle passes through the center of the circle.
One chord of the given circle is the segment with endpoints (0,0) and (5,0). That is a horizontal segment with midpoint (0,2.5); the perpendicular bisector of that segment is the vertical line x=2.5. So the center of the circle lies somewhere on the line x=2.5; the coordinates of the center of the circle are (2.5,y), where y is to be determined.
For a purely algebraic method for finding the center, we can use the fact that the distance from the center to any point on the circle is constant, so the distance from (2.5,y) to (5,0) is the same as the distance from (2.5,y) to (3,3):




The center of the circle is (2.5,0.5).
Use that center point and any of the three given points on the circle to find that the radius of the circle is 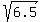 . Then plug the coordinates of the center and the radius in the standard form for the equation of a circle to find the equation is . Then plug the coordinates of the center and the radius in the standard form for the equation of a circle to find the equation is

An alternative algebraic method for finding the center is by finding the intersection of any two chords of the circle.
We have the equation of one chord: x=2.5.
A little algebra shows that the perpendicular bisector of the chord joining (0,0) and (3,3) has the equation y=-x+3; the intersection of those two chords is (2.5,0.5).
I leave the details of those calculations to the student.
ANSWER: 
|
|
|
| |