Question 120519: A plane flies 720 mi against a steady 30-mi/h headwind and then returns to the same point with the wind. If the entire trip takes 10 h, what is the plane’s speed in still air?
Found 2 solutions by stanbon, solver91311:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! A plane flies 720 miles against a steady 30 mph headwind and then returns to the same point with the wind, if the entire trip takes 10 hours what is the plane's speed in still air?
-----------------------
Let "p" be the plane's speed in still air.
--------------------
Upwind DATA;
Distance = 720 miles ; Rate = p-30; time = d/r = 720/(p-30) hrs.
-------------
Downwind DATa:
Distance = 720 miles ; Rate = p+30: time = d/r = 720/(p+30) hrs
--------------
EQUATION:
time up + time down = 10 hrs
720/(p-30) + 720/(p+30) = 10
------------------------
Divide thru by 10 to get:
72/(p-30) + 72/(p+30) = 1
--------------
Multiply thru by (p-30)(p+30)=p^2-900
---------------
72(p+30) + 72(p-30) = p^2-900
144p = p^2-900
p^2-144p-900= 0
(p-150)(p+6) = 0
p = 150 mph (plane speed in still air is 150 mph)
==================
Cheers,
Stan H.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let r be the speed in still air, in accordance with rule one for word problems: Set the variable equal to the thing you want to know.
Air speed against the wind would then be 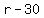 and airspeed with the wind would be and airspeed with the wind would be 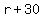 . If the against the wind part of the trip takes t hours, then the return trip must take 10 - t hours, because the entire trip took 10 hours. . If the against the wind part of the trip takes t hours, then the return trip must take 10 - t hours, because the entire trip took 10 hours.
The formula for straight-line distance in terms of constant rate over a period of time is  . So we can express time as a function of distance and rate by saying . So we can express time as a function of distance and rate by saying  . .
In our case, the time for the outbound trip, t, is given by  . The time for the return trip, 10 - t, is given by . The time for the return trip, 10 - t, is given by 
First solve this second equation for t:





Now, note that we have two expressions for t in terms of r. Set them equal to each other:

Multiply by 

Distribute and collect terms


Divide by 10

Note that  and and  , so , so
 => =>  or or 
The solution set to the quadratic is therefore 150 or -6. Since flying backwards doesn't make much sense, exclude the -6 value as an extraneous root. The speed in still air is 150 miles per hour.
Check:
 and and  , and finally, 6 + 4 = 10. Answer checks. , and finally, 6 + 4 = 10. Answer checks.
Hope that helps,
John
|
|
|