Question 1205175: If 𝛼, 𝛽, 𝛾 (where 𝛼, 𝛽, 𝛾 ≠ 0) are the roots of the equation 𝑥
3 + 𝑝𝑥^2 + 𝑞𝑥 + 𝑟 = 0, where 𝑝, 𝑞
and 𝑟 (≠ 0) are real numbers, express the following in terms of 𝑝, 𝑞 and 𝑟:
1/𝛼^3 + 1/𝛽^3 + 1/𝛾^3
Answer by ikleyn(52932)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If 𝛼, 𝛽, 𝛾 (where 𝛼, 𝛽, 𝛾 ≠ 0) are the roots of the equation 𝑥^3 + 𝑝𝑥^2 + 𝑞𝑥 + 𝑟 = 0,
where 𝑝, 𝑞 and 𝑟 (≠ 0) are real numbers, express the following in terms of 𝑝, 𝑞 and 𝑟:
1/𝛼^3 + 1/𝛽^3 + 1/𝛾^3
~~~~~~~~~~~~~~~~~~~~~~~~~~
For simplicity of writing, I will replace  , ,  and and  by "a", "b" and "c". by "a", "b" and "c".
So, we are given an equation 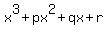 = 0, where p, q and r (=/=0) are real numbers, = 0, where p, q and r (=/=0) are real numbers,
with the roots a, b and c.
They want we find 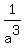 + + 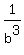 + + 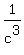 . .
Step by step solution
(a) First, notice that if "a" is the solution to polynomial equation 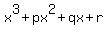 = 0, then = 0, then
 = 0. (1)
Since r =/= 0, the root "a" is also not zero, a =/= 0. In equation (1), divide both sides by = 0. (1)
Since r =/= 0, the root "a" is also not zero, a =/= 0. In equation (1), divide both sides by  .
You will get then .
You will get then
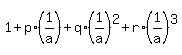 = 0.
It means that = 0.
It means that 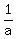 is the root of the cubic polynomial equation is the root of the cubic polynomial equation
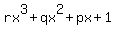 = 0. (2)
Similarly, if "a", "b" and "c" are the roots to equation (1), then = 0. (2)
Similarly, if "a", "b" and "c" are the roots to equation (1), then 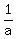 , ,  and and 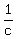 are the roots
of equation (2).
(b) OK. It means that if "a", "b" and "c" are the roots of equation (1), are the roots
of equation (2).
(b) OK. It means that if "a", "b" and "c" are the roots of equation (1), 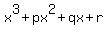 = 0,
they want we calculate = 0,
they want we calculate 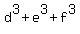 , where d, e, and f are the roots of equation (2), , where d, e, and f are the roots of equation (2), 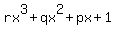 = 0.
(c) Due to Vieta's theorem, if d, e and f are the roots of equation (2), then
d + e + f = = 0.
(c) Due to Vieta's theorem, if d, e and f are the roots of equation (2), then
d + e + f = 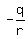 , d*e + d*f + e*f = , d*e + d*f + e*f = 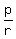 , d*e*f = , d*e*f = 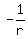 . (3)
(d) For any real numbers d, e, f, the following identity is valid . (3)
(d) For any real numbers d, e, f, the following identity is valid
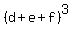 = = 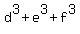 + 3*(d+e+f)*(de + df + ef) - 3def. (4)
It can be checked / proved by direct calculation.
(e) Now, substitute expressions (3) into (4). You will get then + 3*(d+e+f)*(de + df + ef) - 3def. (4)
It can be checked / proved by direct calculation.
(e) Now, substitute expressions (3) into (4). You will get then
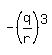 = = 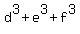 + +  - - 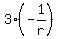 .
It implies .
It implies 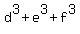 = = 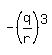 + +  - - 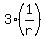 , or , or
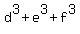 = = 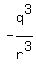 + +  - - 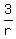 .
(f) Thus the problem is just solved, and the ANSWER is:
if a, b and c are the roots of equation (1), then .
(f) Thus the problem is just solved, and the ANSWER is:
if a, b and c are the roots of equation (1), then 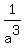 + + 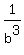 + + 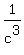 = = 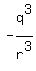 + +  - - 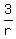 .
ANSWER. If a, b and c are the roots of equation .
ANSWER. If a, b and c are the roots of equation 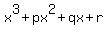 = 0,
then = 0,
then 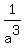 + + 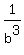 + + 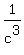 = = 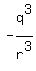 + +  - - 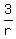 . .
Solved.
|
|
|