SOLUTION: Let D and E be the following matrices: I don't know how to format matrices on here, so I will write the top row (horizontal) and the bottom row. These are all 2 x 2 matrices.

Algebra ->  Matrices-and-determiminant -> SOLUTION: Let D and E be the following matrices: I don't know how to format matrices on here, so I will write the top row (horizontal) and the bottom row. These are all 2 x 2 matrices.       Log On


   

Question 1205107: Let D and E be the following matrices:
I don't know how to format matrices on here, so I will write the top row (horizontal) and the bottom row. These are all 2 x 2 matrices.
D dilates vectors by a factor of 3. E is the matrix [1 2][4 5].
Calculate the matrix D^-1 E[-2 1][1 4]
Sorry if the matrices are unclear. In latex, you are calculating $\[\mathbf{D}^{-1}\mathbf{E} \begin{pmatrix} -2 & 1\\ 1 & 4 \end{pmatrix}.\]$
Found 3 solutions by ikleyn, kately, math_tutor2020:
Answer by ikleyn(52871) About Me  (Show Source):
You can put this solution on YOUR website!
.

Since D dilates vectors by the factor 3,

    D = %28matrix%282%2C2%2C+3%2C0%2C+0%2C3%29%29.


Hence,  D%5E%28-1%29 = %28matrix%282%2C2%2C+1%2F3%2C0%2C+0%2C1%2F3%29%29.


The rest is mechanical job of multiplying matrices.



Answer by kately(2) About Me  (Show Source):
You can put this solution on YOUR website!
Thank you to ikleyn! Using D^-1, I got that the final answer was [0 9][-3 24].

Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

D+=+%28matrix%282%2C2%2C3%2C0%2C0%2C3%29%29
This matrix D scales any vector (x,y) to (3x,3y), i.e. any vector is now 3 times longer than before.

D%5E%28-1%29+=+%28matrix%282%2C2%2C1%2F3%2C0%2C0%2C1%2F3%29%29
We invert each of the diagonal entries. This applies to diagonal matrices only.

Notice how
D%2AD%5E%28-1%29+=+D%5E%28-1%29%2AD+=+I+=+%28matrix%282%2C2%2C1%2C0%2C0%2C1%29%29

Then use matrix multiplication to find that D%5E%28-1%29%2AE+=+%28matrix%282%2C2%2C1%2F3%2C+2%2F3%2C+4%2F3%2C+5%2F3%29%29

Furthermore, you should find that

I used GeoGebra's CAS feature to confirm the answer is correct. There are many similar alternatives.

To write out matrix notation on a keyboard, you could write something like 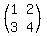%28matrix%282%2C2%2C1%2C2%2C3%2C4%29%29 as {{1,2},{3,4}} which is how GeoGebra and WolframAlpha handle matrices.
Or you can use Matlab's notation of [1,2;3,4] where the semicolon tells when to make a new row. There are probably other styles of notation.

LaTex notation is acceptable assuming it's properly formatted. The only drawback is that it might be tricky to decipher (even if someone is very familiar with LaTex); but the good news is that there are online LaTex editors to translate.
Personally a style like [1,2;3,4] should suffice.