Question 1205032: If sin(x)=-5/13 and x is in quadrant III, with 0° ≤ x < 360°, find the exact values of the expressions without solving for x.
sin(x/2)
cos(x/2)
tan(x/2)
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! If sin(x)=-5/13 and x is in quadrant III,...
So for angle x, we have a 5-12-13 right triangle in quadrant III,
where x=-12, y=-5, and r=+13.
There is often a conflict of notation when x is used for an angle, and also
for values of the adjacent side of the defining right triangle. There is a
problem here. But I think you won't get confused. Teachers aren't always
careful to point out this conflict, which happens a lot. (just like the problem
of how to say "the sign of the sine". J )
So cos(x)=x/r=(-12)/(+13)=-12/13 and tan(x)=y/x=(-5)/(-12)=+5/12
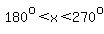
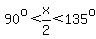 so x/2 is in quadrant II (the upper half of quadrant II).
So sin(x/2) is positive, cos(x/2) is negative, and tan(x/2) is negative.
So we just use the half-angle formulas: so x/2 is in quadrant II (the upper half of quadrant II).
So sin(x/2) is positive, cos(x/2) is negative, and tan(x/2) is negative.
So we just use the half-angle formulas:
 , ,  We know to use the + because x/2 is in quadrant II, where sine is positive.
We know to use the + because x/2 is in quadrant II, where sine is positive.
 We know to use the - because x/2 is in quadrant II, where cosine is negative.
We know to use the - because x/2 is in quadrant II, where cosine is negative.
 Now we could use a formula for tan(x/2), but now all we need is
Now we could use a formula for tan(x/2), but now all we need is 
 Edwin
Edwin
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If sin(x)=-5/13 and x is in quadrant III, with 0° ≤ x < 360°, find the exact values of the expressions without solving for x.
sin(x/2)
cos(x/2)
tan(x/2)
~~~~~~~~~~~~~~~~~~~~
As the problem is worded, printed and presented in the post, it has a shocking deficiency.
One part says that x is in quadrant III, and then next part says 0° ≤ x < 360°,
which is INCONSISTENT writing (making a reader tremble in horror).
There are two ways to fix it and to present it correctly/consistently.
One way is to omit this inequality 0° ≤ x < 360°.
Other way is to write 180° ≤ x < 270°.
As it is seen from the post, the math composer is quite illiterate in writing Math.
*********************************************************************
I am writing these lines in order for to prevent this formulation
to go out in the Internet for spreading/distribution in this form
as it is presented in the post.
*********************************************************************
With friendly greetings.
|
|
|