SOLUTION: The 5th term of a GP is 8, the third term is 4, and the sum of the first ten terms is positive. Find the first term, the common ratio, and the sum of the first Ten years

Algebra ->  Sequences-and-series -> SOLUTION: The 5th term of a GP is 8, the third term is 4, and the sum of the first ten terms is positive. Find the first term, the common ratio, and the sum of the first Ten years       Log On


   

Question 1205015: The 5th term of a GP is 8, the third term is 4, and the sum of the first ten terms is positive. Find the first term, the common ratio, and the sum of the first Ten years
Found 3 solutions by MathLover1, ikleyn, greenestamps:
Answer by MathLover1(20850) About Me  (Show Source):
Answer by ikleyn(52790) About Me  (Show Source):
You can put this solution on YOUR website!
.
The 5th term of a GP is 8, the third term is 4, and the sum of the first ten terms is positive.
Find the first term, the common ratio, and the sum of the first ten highlight%28cross%28years%29%29 terms.
~~~~~~~~~~~~~~~~~ 

    a%5B5%5D = 8

    a%5B3%5D = 4

implies

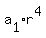    a%5B1%5D%2Ar%5E4 = 8    (1)

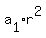    a%5B1%5D%2Ar%5E2 = 4    (2)


Divide equation (1) by equation (2)  (both sides).  You will get

    r%5E2 = 2,  r = +/- sqrt%282%29.


Let's consider case  r = sqrt%282%29  first  (positive value).  We then have

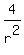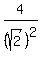    a%5B1%5D = 4%2Fr%5E2 = 4%2F%28sqrt%282%29%29%5E2 = 4%2F2 = 2.

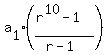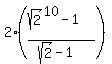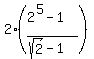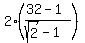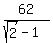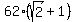    S%5B10%5D = a%5B1%5D%2A%28%28r%5E10-1%29%2F%28r-1%29%29 = 2%2A%28%28sqrt%282%29%5E10-1%29%2F%28sqrt%282%29-1%29%29 = 2%2A%28%282%5E5-1%29%2F%28sqrt%282%29-1%29%29 = 2%2A%28%2832-1%29%2F%28sqrt%282%29-1%29%29 = 62%2F%28sqrt%282%29-1%29 = 62%2A%28sqrt%282%29%2B1%29.


Now, if  r = -sqrt%282%29%29, then the sum  S%5B10%5D will be, OBVIOUSLY, negative; so, due to the condition, we reject this case.


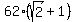ANSWER.  a%5B1%5D = 2;  r = sqrt%282%29,  S%5B10%5D = 62%2A%28sqrt%282%29%2B1%29.

Solved.

///////////////////

Sorry, by mistake, I overlayed the post by @MathLover1 by my post . . .

I regret very much, sorry . . .




Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


The 3rd term 4 is half of the 5th term 8, so the 1st term is half of the 3rd term, so the first term is 2.

From the given information, the common ratio could be either sqrt(2) or -sqrt(2)

But if the common ratio were negative, the sum of the first two terms would be negative, as would each sum of any following two terms, making the sum of the first ten terms negative.

So the common ratio is sqrt(2).

In the sum of the first ten terms, the sum of the odd-numbered terms is 2+4+8+16+32 = 62; so the sum of the even-numbered terms is 62*sqrt(2).

ANSWERS:
common ratio: sqrt(2)
sum of first ten terms: 62+62*sqrt(2)