|
Question 1204998: Given n ≥ 1,(Mn×n(R), +, -) is a real vector space, where Mn×n(R) is the set of n × n matrices at real coefficients, (+) is the sum of matrices and (-) is the product of a matrix by a real number.
Consider the following set of the vector space of 3 × 3 matrices: W = {A∈ M3×3(R) | τ (A) = 0}
1.Prove that W is a vector subspace of M3×3(R).
2.Find a basis B of W.
3. Calculate the dimension of W
Answer by ikleyn(52884)   (Show Source):
You can put this solution on YOUR website! .
Given n ≥ 1,(Mn×n(R), +, -) is a real vector space, where Mn×n(R) is the set of n × n matrices at real coefficients,
(+) is the sum of matrices and (-) is the product of a matrix by a real number.
Consider the following set of the vector space of 3 × 3 matrices: W = {A∈ M3×3(R) | τ (A) = 0}
1.Prove that W is a vector subspace of M3×3(R).
2.Find a basis B of W.
3. Calculate the dimension of W
~~~~~~~~~~~~~~~~~~~~~
This task is, obviously, for the University student learning linear algebra (or abstract algebra).
So, I will assume that this person is adequately prepared and has adequate basic knowledge on the subject.
Therefore, I will give (will provide) general / basic instructions without going in details
and without chewing the material.
Before to start, I will make couple of notices on problem's formulation.
(a) since we are talking about matrices, the case n= 1 should be EXCLUDED from consideration;
therefore, actually n > 1 in this problem.
(b) τ (A) is the trace of a matrix A, i.e. the sum of its diagonal elements.
Standard designation for it is Tr(A) or tr(A).
Now to the SOLUTION.
I will answer questions in this order (3), (1), (2).
(3) The space of all 3x3 matrices over R has the dimension of 3x3 = 9.
Our sub-space W is obtained from this 9D space by imposing one restriction tr(A) = 0;
Hence, the sub-space W has the dimension of 9-1 = 8.
(1) The trace function of matrices has this property tr(a*A + b*B) = a*tr)A) + b*tr(B),
where "a" and "b" are real numbers; "A" and "B" are nxn-matrices. The proof is obvious
(and is in any relevant textbook on the subject).
Therefore, if tr(A) = 0 and tr(B) for 3x3 matrices A and B from our sub-space, then
tr(a*A + b*B) = a*tr(A) + b*tr(b) = a*0 + b*0 = 0; hence, the matrix a*A + b*B belongs
to the same subspace.
It proves that the set of matrices defined in (1) is a linear sub-space.
(2) One basis of the subspace W is THIS set
- it includes n*(n-1) = n^2 - n = 3^2-3 = 9-3 = 6 matrices  , that have all elements zero
except the element 1 in the out-the-diagonal cell (i,j), {1 <= i <= 3, 1 <= j <= 3, i=/=j}
PLUS / (add) this set of two diagonal matrices
 =  ,  =  .
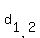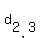It is obvious that these 8 matrices are linearly independent over real numbers;
hence, these 8 matrices form a basis in our 8D subspace W.
Solved.
|
|
|
| |
