.
Write the complex number in polar form.
-1/8 - 1/8i
~~~~~~~~~~~~~~~~~~~~~~~
The point is in quadrant III, QIII.
The module is r =  =
= 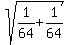 =
=  =
= 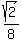 .
The argument is
.
The argument is  =
= 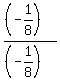 = 1.
Therefore, the angle (the argument) is
= 1.
Therefore, the angle (the argument) is  =
=  , or 135 degrees.
So, the polar form for the point is (r,
, or 135 degrees.
So, the polar form for the point is (r, ) = (
) = (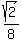 ,
, ).
The complex number in polar form is z =
).
The complex number in polar form is z = 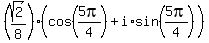 .
.
Solved.