Question 1204819: If 5 -letter
words'' are formed using the letters A, B, C, D, E, F, G, how many such words are possible for each of the following conditions:
(a) No condition is imposed.
Your answer is :
(b) No letter can be repeated in a word.
Your answer is :
(c) Each word must begin with the letter A and letters can be repeated.
Your answer is :
(d) The second letter must be a vowel and no letters can be repeated.
Your answer is :
Found 3 solutions by MathLover1, math_tutor2020, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! If 5 -letter words are formed using the letters  , ,  , ,  , ,  , ,  , ,  , , 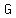 , how many such words are possible for each of the following conditions: , how many such words are possible for each of the following conditions:
(a) No condition is imposed.
There are  choices for the first letter. choices for the first letter.
There are  choices for the second letter choices for the second letter
There are  choices for the third letter. choices for the third letter.
There are  choices for the fourth letter choices for the fourth letter
There are  choices for the fifth letter. choices for the fifth letter.
The total number of  -letter words possible: -letter words possible:

Your answer is : 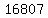
(b) No letter can be repeated in a word.
For the first letter, there are  choices. choices.
For the second letter, there are only  choices left (since we cannot repeat the first letter). choices left (since we cannot repeat the first letter).
For the third letter there are  choices. choices.
For the fourth letter there are  choices. choices.
For the fifth letter there are 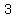 choices. choices.
The total number of  -letter words possible with no letter repeated: -letter words possible with no letter repeated:

Your answer is : 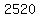
(c) Each word must begin with the letter  and letters can be repeated. and letters can be repeated.
For the first letter, there is only  choice (the letter choice (the letter  ). ).
For the second letter there are  choices (since any letter can be used). choices (since any letter can be used).
For the third letter there are  choices, for the fourth letter there are choices, for the fourth letter there are  choices, and for the fifth letter there are choices, and for the fifth letter there are  choices. choices.
The total number of  -letter words is possible with the first letter being -letter words is possible with the first letter being  : :

Your answer is : 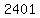
(d) The second letter must be a vowel and no letters can be repeated.
For the first letter, there are  choices (since any letter can be used). choices (since any letter can be used).
For the second letter, there are  choices (the vowels choices (the vowels  , and , and  ). ).
For the third letter there are  choices, for the fourth letter there are choices, for the fourth letter there are  choices, and for the fifth letter there are choices, and for the fifth letter there are  choices. choices.
The total number of  -letter words possible with the second letter being a vowel: -letter words possible with the second letter being a vowel:

Your answer is : 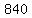
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answers:
(a) 16807
(b) 2520
(c) 2401
(d) 720
------------------------------------------------
------------------------------------------------
Explanation for part (a)
There are 7 letters in the set {A,B,C,D,E,F,G}
When no condition is imposed, we can repeat letters.
There are 7 choices and 5 slots to fill. Giving 7^5 = 16807 different words possible.
Most of these "words" won't be found in the dictionary, but are simply strings of the letters mentioned.
------------------------
Explanation for part (b)
Unlike the previous part, we cannot repeat letters here.
There are 7 choices for the first slot, then 6 for the next slot, and so on.
We have 7*6*5*4*3 = 2520 different permutations possible.
Alternatively, use the nPr formula with n = 7 and r = 5.
------------------------
Explanation for part (c)
The first slot is locked to letter A.
The remaining 4 letters can be anything of the set {A,B,C,D,E,F,G} where repeats are allowed.
The logic is similar to part (a) we've done earlier.
We have 7^4 = 2401 different words that start with A when repeat letters are allowed.
------------------------
Explanation for part (d)
Given set = {A,B,C,D,E,F,G}
vowels from that set = {A, E}
There are 2 choices for the second slot (either A or E)
There are 7-1 = 6 choices for the first slot, due to one of the vowels already taken.
Then 6-1 = 5 choices for the third slot, 5-1 = 4 choices for the fourth slot, and 4-1 = 3 choices for the last slot.
6*2*5*4*3 = 720 permutations where a vowel is the second letter.
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For part (d), the solution and the answer in the post by @MathLover1 are incorrect.
The correct solution is as follows
2 options for the 2nd letter (A or E);
7-1 = 6 options for 1st letter;
5 options for 3rd positions;
4 options for 4th position;
3 options for last, 5th position.
In all, 2*6*5*4*3 = 720 different options are possible. ANSWER for (d)
|
|
|