Question 1204795: If a,b,c,d, and e are distinct prime numbers such that: b=(a-1)^1/2 +1 ; c=(b-1)^1/2 +1 ; d=(c-1)^1/2 +1 ; e= (d-1)^1/2 +1 ; Find the least possible value of a+b+c+d+e
A) 65537
B) 65536
C) 65816
D) 65819
E) 65814
Found 3 solutions by MathLover1, ikleyn, math_tutor2020:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!




Find the least possible value of 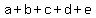
A Fermat number is of the form
 . .
 , ,  , ,  , ,  , ,  are are 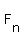 for for  = { = {  , ,  , ,  , ,  } }





so,  , ,  , ,  , ,  , and , and  are the five known prime Fermat numbers (in descending order) are the five known prime Fermat numbers (in descending order)
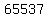 , , 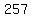 , ,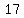 , ,  , and , and  . .
their sum is:

answer:
D) 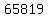
Answer by ikleyn(52834)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It was just solved at this forum several/many years ago.
See the link
https://www.algebra.com/algebra/homework/Expressions-with-variables/Expressions-with-variables.faq.question.1168701.html
@MathLover1 copy-pasted from that source without reference, as she usually does it.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I'm assuming that b=(a-1)^1/2 +1 should be the equation b=(a-1)^(1/2) +1, which is the same as writing  and converts to and converts to 
List of the first few primes = {2,3,5,7,11,13,17,19,23,29,31,...}
There are infinitely many prime numbers.
Let's say we picked the smallest prime for value "e".
Doing so will guarantee that a+b+c+d+e is minimized.
e = (d-1)^(1/2) + 1
(d-1)^(1/2) = e-1
d-1 = (e-1)^2
d = (e-1)^2 + 1
d = (2-1)^2 + 1
d = 2
e = 2 leads to d = 2
But d must be different from e, so we have to go back to the drawing board.
Let's pick the next largest prime.
e = 3
d = (e-1)^2 + 1
d = (3-1)^2 + 1
d = 5
We get a different value this time. So far so good.
Furthermore, the result is prime.
Then,
d = (c-1)^(1/2) + 1
c = (d-1)^2 + 1
c = (5-1)^2 + 1
c = 17
We get a different prime.
And,
c = (b-1)^(1/2) + 1
b = (c-1)^2 + 1
b = (17-1)^2 + 1
b = 257
which is also prime.
Primality can be checked using software. Or you can check the primes {2,3,5,7,11,13} to find they aren't factors of 257.
And lastly,
b = (a-1)^(1/2) + 1
a = (b-1)^2 + 1
a = (257-1)^2 + 1
a = 65537
This value is prime.
Use software to check primality.
To summarize
a = 65537
b = 257
c = 17
d = 5
e = 3
all of which are different primes and fit the equations mentioned.
This is the smallest set possible since e = 3 was chosen among the smallest primes.
So,
a+b+c+d+e = 65537+257+17+5+3 = 65819 is the smallest sum possible, which leads to answer choice D
|
|
|