Question 120479: Find a counterexample to show that the following statement is incorrect:
“The sum of any two odd numbers is divisible by 4”
Found 2 solutions by stanbon, MathLover1:
Answer by stanbon(75887)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! show that the following statement is 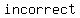 : :
“ 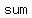 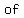   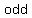  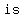  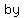  ." ."
first recall some of 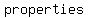 relating to relating to  numbers: numbers:
-All odd numbers can be expressed as 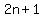 where where  is a whole number. is a whole number.
-Sum or difference of   numbers is numbers is 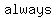 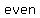 . .
-Sum of 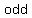 and and  number is number is 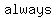 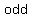 . .
also recall that:
-A number 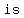  by by  , when the number formed by the last two right hand digit is divisible by , when the number formed by the last two right hand digit is divisible by  . .
-Or, a number is 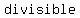 by by  , if its two last digits are , if its two last digits are 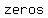 or they make a or they make a 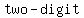 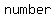 , which is divisible by , which is divisible by  . .
Any integer  can be put into can be put into 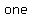 of the four cases of the four cases 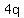 , ,  , , 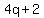 , and , and 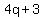 . .
Since 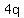 and and 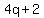 are are  , only the cases , only the cases  and and 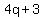 need be considered. need be considered.
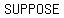 that that 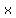 is the is the 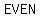 number. Then number. Then  has a factor of has a factor of  and and  has a factor of has a factor of  ; that is, ; that is,  is divisible by is divisible by  . .
If we choose  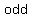 numbers, let’s say numbers, let’s say  and and  , and , and 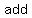 their squares ( their squares (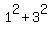 in this case) we will find that the in this case) we will find that the  is is   by by  . .
 …. …. …… => .. …… => ..  by by  . .
If and and  are are 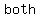  they have the form they have the form  and and  . .
Then  , which has a , which has a 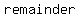 of of  when divided by when divided by  and so can not be equal to and so can not be equal to  , which is exactly divisible by , which is exactly divisible by  . .
Therefore the 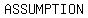 that that  is is 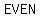 is is 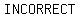 . .
Since 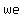 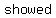 that that 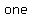 of the terms of the terms   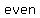 , one of , one of  and and    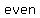 , and , and 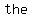 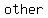 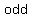 . .
|
|
|