Question 1204733: Find the coordinates of the focus and the vertex, the equations of the directrix and the axis of symmetry, and the direction of opening of the parabola.
2y^2 + 16x = 16y - 64
-----------
I don’t know what I’m doing wrong. I keep getting (-2,4) for the vertex, even though the answer I was given is (-6,4)
Found 3 solutions by josgarithmetic, ikleyn, MathLover1:
Answer by josgarithmetic(39620)   (Show Source):
Answer by ikleyn(52798)  (Show Source):
You can put this solution on YOUR website! .
I also do not know what you are doing wrong, since you do not show it to us.
But you may check that the point (-6,4) does not lie on this curve, at all,
since its coordinates do not satisfy the given equation.
So, the answer given to you is DEFINITELY WRONG
(if this answer does relate to vertex).
Answer by MathLover1(20850)  (Show Source):
You can put this solution on YOUR website!
If a parabola has a horizontal axis, the standard form of the equation of the parabola is this:
 , where  .
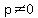The vertex of this parabola is at ( , ).
The focus is at ( ,  ).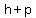
 ... first simplify, divide by 
 ...move  term to the left side and  to the right side
 ...complete square on left side
V(,)=( , )
F(, )=( , )=( ,)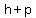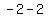
so, your answer is correct
check if ( ,) is on parabola
 => evidently false, so (,) is NOT on parabola
|
|
|
