Question 1204718: Suppose that 10 years ago you bought a home for $150,000, paying 10% as a down payment, and financing the rest at 8% interest for 30 years. How much money did you pay as your down payment?
How much money was your existing mortgage (loan) for?
What is your current monthly payment on your existing mortgage?Carry at least 4
decimal places during calculations, but round your final answer to the nearest cent.
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52765)   (Show Source):
You can put this solution on YOUR website! .
Suppose that 10 years ago you bought a home for $150,000, paying 10% as a down payment,
and financing the rest at 8% interest for 30 years. How much money did you pay as your down payment?
(a) How much money was your existing mortgage (loan) for?
(a) What is your current monthly payment on your existing mortgage?Carry at least 4
decimal places during calculations, but round your final answer to the nearest cent.
~~~~~~~~~~~~~~~~~~~~~~~~
(a) Down payment was 10$ of $150,000, or $15,000. ANSWER to question (a)
(b) The loaned amount was $150,000 - $15,000 = $135,000.
To find monthly payment P, use the standard formula
P =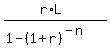 
where L is the loan amount;
r is the nominal interest rate per month as a decimal;
n is the number of months (the number of equal monthly payments).
In this problem
L = $135,000;
r = 0.08/12;
n = 30*12 = 360 months.
The calculations are here
P = 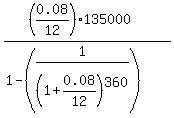 = 990.58 dollars. ANSWER to question (b)
You may check these calculations using online calculators
https://www.calculator.net/loan-calculator.html
or
https://www.calculatorsoup.com/calculators/financial/loan-calculator.php
Solved.
Answer by math_tutor2020(3816)  (Show Source):
You can put this solution on YOUR website!
Answers:
Down payment = $15,000
Loan amount = $135,000
Monthly payment = $990.58
Work Shown
down payment = 10% of home value
down payment = 10% of $150,000
down payment = 0.10*($150,000)
down payment = $15,000
Basically chop a 0 off at the end.
loan amount = home value - down payment
loan amount = $150,000 - $15,000
loan amount = $135,000
Or
loan amount = 90% of home value
loan amount = 0.90*($150,000)
loan amount = $135,000
This is the starting balance of the mortgage.
Monthly payment formula
P = (L*i)/( 1-(1+i)^(-n) )
where,
P = monthly payment
L = loan amount
i = monthly interest rate in decimal form
n = number of months
In this case
P = unknown = what we want to calculate
L = 135000
i = 0.08/12 = 0.00666667 approximately
n = 30*12 = 360 months
P = (L*i)/( 1-(1+i)^(-n) )
P = (135000*0.00666667)/( 1-(1+0.00666667)^(-360) )
P = 990.582551181798
P = 990.58
Many online calculators such as this one
https://www.calculator.net/loan-calculator.html
can be used to verify the correct monthly payment.
Here's what it looks like if we vary the precision on the value of 'i'
| # of decimal digits | i = monthly rate in decimal form | monthly payment | | 3 | 0.007 | 1028.48 | | 4 | 0.0067 | 994.35 | | 5 | 0.00667 | 990.96 | | 6 | 0.006667 | 990.62 | | 7 | 0.0066667 | 990.59 | | 8 | 0.00666667 | 990.58 | | 9 | 0.006666667 | 990.58 | | 10 | 0.0066666667 | 990.58 | | 11 | 0.00666666667 | 990.58 | | 12 | 0.006666666667 | 990.58 |
As you can see, 4 decimal digits is not enough. We must use 8 decimal digits or more. Storing the value of i into the calculator will let the calculator handle the precision level.
|
|
|
