Question 1204716: Find the number of distinguishable permutations of the given letters "AAABBBCD".
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! permutations of {  , ,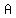 , ,  , ,  , ,  , , , ,  , ,  } }
there are  letters letters
there are   s and s and   s, since order matters, there will be following number of permutations : s, since order matters, there will be following number of permutations :
 /( /(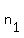 * *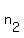 *....* *....*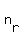 ) )

Distinct subsets:
Subsets :  ; ;  ; ;  ; ;  ; ;
Subsets' count:  , ,  , ,  , , 

The letters of the word 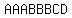 can be arranged in can be arranged in  distinct ways. distinct ways.
Answer by ikleyn(52921)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the number of distinguishable permutations of the given letters "AAABBBCD".
~~~~~~~~~~~~~~~~~~~~~~~~~
The formula for the number of distinguishable permutations of this word is
n = 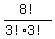 . (1)
In this formula, 8! reflects the number of all permutations of 8 letters in the word.
First 3! in the denominator reflects three repeating letters A in it.
Second 3! in the denominator reflects three repeating letters B in the word.
The ANSWER is, according to formula (1), n = 1120. . (1)
In this formula, 8! reflects the number of all permutations of 8 letters in the word.
First 3! in the denominator reflects three repeating letters A in it.
Second 3! in the denominator reflects three repeating letters B in the word.
The ANSWER is, according to formula (1), n = 1120.
Solved.
----------------
To see many other similar (and different) solved problems, look into the lesson
- Arranging elements of sets containing indistinguishable elements
in this site.
Learn the subject from there.
|
|
|