|
Question 1204699: Write the equation for the hyperbola in standard form and general form.
center (4,0), one vertex (2,0), slope of one asymptote 3/2
----------
As I understood for the standard form equation, a^2 is always in the first denominator and b^2 always in the second denominator for hyperbolas and that (x-h)^2 in the first numerator represents a horizontal transverse axis whereas (y-k)^2 in the first numerator represents a vertical transverse axis.
I think the asymptote equations are y = k +- b/a(x-h) for horizontal transverse axis and y = k +- a/b(x-h) for vertical transverse axis. But I am still confused. When I’m given a slope like 3/2, what does that mean for the values of a and b? Is 3/2 the same as the “+-b/a” in an asymptote equation? Or is it 2/3? I know that a slope (m) = y2-y1 / x2-x1, but the use of a/b or b/a in the asymptote formula and how a or b can both be in the denominator of either (x-h)^2 or (y-k)^2 depending on whether transverse axis is horizontal or vertical has muddled everything in my head. What I think I’m trying to say is that rise/run (y2-y2/x2-x1) vs b/a and b/a and how they relate to y and x in the slope and a and b in the standard form equations is causing me confusion.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The center of a hyperbola is ( , , ), so ( ), so ( , ,  )=( )=( , , ) => ) =>  , , 
One of the vertices is ( , , ), the same ordinate as the center, so we have hyperbola with a horizontal transverse axis. ), the same ordinate as the center, so we have hyperbola with a horizontal transverse axis.
For a hyperbola with a horizontal transverse axis, the relationship between the center and vertex is as follows:
vertex is at ( , , )=( )=(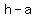 , , ) )
so, 
since  , we have , we have



For a hyperbola with a horizontal transverse axis, the slope of the asymptotes is
 =± =±
if given slope  and and  , we have , we have
 => =>
The equation of the hyperbola in standard form with a horizontal transverse axis is

substitute all the components

 =>your answer =>your answer

|
|
|
| |