|
Question 1204680: For the hyperbola, determine the
a) coordinates of the center
b) directions and lengths of both axes
c) coordinates of the vertices
d) slopes of the asymptotes
https://i.ibb.co/6YZnZHT/1.jpg
I don’t know why this graph is confusing me. It could be the seemingly asymmetric look of the asymptotes. I don’t know how to trace a box in the center with asymptotes that appear slanted and the two parts of the hyperbola that appear different to me.
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!
The standard form of the equation of a hyperbola with center ( ,) and transverse axis on the  -axis is
we know that the coordinates of the center are
( , )=(,)
and the vertices are
( ,)=( ,) and ( ,)=( ,)
=> 
since the transverse axis is horizontal, asymptote formula will be:
 =±
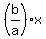
from graph we see that one asymptote passes through the origin (,) and (, )
slope is:
equation is:
the other asymptote passes through origin and point (, )
slope is:
equation is:
then, since =±,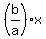 
and your equation of hyperbola is:
For the hyperbola, determine the
a) coordinates of the center
(,)
b) directions and lengths of both axes
the transverse axis is horizontal
the length of the axes is  and the length of conjugate axis is 
c) coordinates of the vertices
(,) and (,)
d) slopes of the asymptotes
from graph we see that one asymptote passes through the origin (,) and (,)
slope is:
equation is:
the other asymptote passes through origin and point (,)
slope is:
equation is:
|
|
|
| |
