Question 1204648: Suppose a and b are positive numbers for which 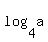 = = 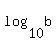 = = 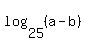 What is the value of b/a? What is the value of b/a?
Answer by ikleyn(52898)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose a and b are positive numbers for which 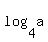 = = 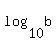 = = 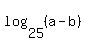 . .
What is the value of b/a?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x be the common value of 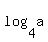 , , 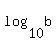 and and 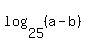 .
So, x = .
So, x = 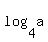 , (1)
x = , (1)
x = 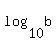 , (2)
x = , (2)
x = 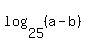 . (3)
Then we can write . (3)
Then we can write
 = a (4) = a (4)
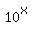 = b (5) = b (5)
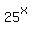 = a-b (6)
Multiply equation (4) by = a-b (6)
Multiply equation (4) by  (both sides). You will get (both sides). You will get
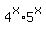 = = 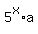 , or , or
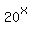 = = 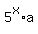 . (7)
Divide equation (7) by equation (5) (side by side). You will get . (7)
Divide equation (7) by equation (5) (side by side). You will get
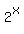 = = 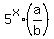 hence
hence
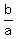 = =  . (8)
Square equation (8) (both sides). You will get . (8)
Square equation (8) (both sides). You will get
 = = 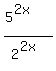 = = 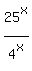 . (9)
Now in the right side of (9) replace . (9)
Now in the right side of (9) replace 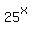 by (a-b), based on (6);
and replace by (a-b), based on (6);
and replace  by "a", based on (4).
You will get then by "a", based on (4).
You will get then
 = =  ,
or ,
or
 = =  . (10)
We just are on the finish line and will celebrate a victory soon.
Now you see that (10) is a quadratic equation for . (10)
We just are on the finish line and will celebrate a victory soon.
Now you see that (10) is a quadratic equation for  .
To solve it quickly for .
To solve it quickly for  , let's introduce new variable , let's introduce new variable  = t.
Equation (10) takes the form
t^2 = 1 - t,
or
t^2 + t - 1 = 0.
Use the quadratic formula = t.
Equation (10) takes the form
t^2 = 1 - t,
or
t^2 + t - 1 = 0.
Use the quadratic formula
 = = 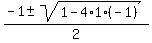 = = 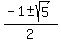 .
Thus we have two solutions for t. But since the numbers "a" and "b" are positive (according to the condition),
we leave only one, positive solution:
t = .
Thus we have two solutions for t. But since the numbers "a" and "b" are positive (according to the condition),
we leave only one, positive solution:
t =  = =  .
ANSWER. There is one and only one solution for .
ANSWER. There is one and only one solution for  . It is . It is  = =  . .
Solved.
///////////////////////
In students' jargon, this problem is a coffin, that is, solving it seems impossible.
However, at this forum you can get a solution even for such a grave task.
Do not forget to post your " THANKS " to me for my teaching.
When you will post your " THANKS ", please refer to the ID number
of this problem, which is 1204648.
|
|
|