SOLUTION: If sin(x) = − 20 29 and x is in quadrant III, with 0° ≤ x < 360°, find the exact values of the expressions without solving for x. (a) sin x 2 (b)

Algebra ->  Trigonometry-basics -> SOLUTION: If sin(x) = − 20 29 and x is in quadrant III, with 0° ≤ x < 360°, find the exact values of the expressions without solving for x. (a) sin x 2 (b)       Log On


   

Question 1204627: If
sin(x) = −
20
29
and x is in quadrant III, with 0° ≤ x < 360°, find the exact values of the expressions without solving for x.
(a)
sin
x
2


(b)
cos
x
2


(c)
tan
x
2
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
If
sin%28x%29+=+-20%2F29and x+is in quadrant III, with 0+%3C=+x+%3C+360°, find the exact values of the expressions without solving for x.

in Q III both sin and cos are negative
we also know that sin%5E2%28x%29%2B+cos%5E2%28x%29=1

solve for cos%28x%29

cos%28x%29=sqrt%281-sin%5E2%28x%29%29

substitute given value of sin%28x%29

cos%28x%29=sqrt%281-%28-20%2F29%29%5E2%29
cos%28x%29=sqrt%281-400%2F841%29
cos%28x%29=sqrt%28441%2F841%29
cos%28x%29=21%2F29 or cos%28x%29=-21%2F29
we need cos%28x%29=-21%2F29


(a) use Half-Angle Identities
sin%28x%2F2%29=sqrt%28%281-cos%28x%29%29%2F2%29
​
sin%28x%2F2%29=sqrt%28%281-%28-21%2F29%29%29%2F2%29
sin%28x%2F2%29=sqrt%28%2850%2F29%29%2F2%29
sin%28x%2F2%29=sqrt%2825%2F29%29
sin%28x%2F2%29=%285sqrt%2829%29%29%2F29 or sin%28x%2F2%29=-%285sqrt%2829%29%29%2F29
in Q III
sin%28x%2F2%29=-%285sqrt%2829%29%29%2F29


(b)

cos%28x%2F2%29=sqrt%28%281%2Bcos%28x%29%29%2F2%29
cos%28x%2F2%29=sqrt%28%281%2B%28-21%2F29%29%29%2F2%29
cos%28x%2F2%29=sqrt%284%2F29%29
cos%28x%2F2%29=%282sqrt%2829%29%29%2F29 or cos%28x%2F2%29=-%282sqrt%2829%29%29%2F29
in Q III
cos%28x%2F2%29=-%282sqrt%2829%29%29%2F29

(c)
tan%28x%2F2%29=%281-cos%28x%29%29%2F%281%2Bcos%28x%29%29
tan%28x%2F2%29=sqrt%28%281-%28-21%2F29%29%29%2F%281%2B%28-21%2F29%29%29%29
tan%28x%2F2%29=sqrt%2825%2F4%29
tan%28x%2F2%29=5%2F2 or tan%28x%2F2%29=-5%2F2
In the third quadrant, the values for tan are positive only.
tan%28x%2F2%29=+5%2F2



Answer by ikleyn(52804) About Me  (Show Source):
You can put this solution on YOUR website!
.

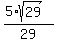In the post by @MathLover1, her answer to (a),  sin%28x%2F2%29 = -%285%2Asqrt%2829%29%29%2F29%29, is incorrect.

To determine the correct answer, we should analyze in which quadrant the angle x%2F2 lies.

Since angle x is in QIII, we conclude that x%2F2 lies in QII.

Hence,  sin%28x%2F2%29  must be POSITIVE  in this problem.

THEREFORE, the correct answer to (a) is  sin%28x%2F2%29 = %285%2Asqrt%2829%29%29%2F29%29,

           the opposite number to the answer by @MathLover1.




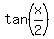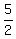Similarly, in her post, the answer to (c),  tan%28x%2F2%29 = 5%2F2%29, is incorrect.

Again, the angle x%2F2  lies in QII, where  tangent is always negative.

THEREFORE, the correct answer to (c) is 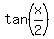 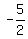tan%28x%2F2%29 = -5%2F2%29,

           the opposite number to the answer by @MathLover1.

--------------------

Hello, could you take care about your posts, in order for they come in good format ?

For it, you should STOP copy-paste from your source, since it does not work properly.

You should print your posts manually using your keyboard and supporting the rules of mathematical grammar.