SOLUTION: A company has $33600 to spend on the development and promotion of a new product. The company estimates that if x is spent on development and y is spent on promotion, then approxima

                      Solution


Let  u = (x^(1/2))*(y^(3/2))/400000 be the given function;

     v = (x^(1/2))*(y^(3/2));

     w = .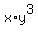


It is obvious that "u" and "v" have the maximum at the same point (x,y)
(dividing by the constant value 400,000 does not shift the position of maximum on (x,y)-plane).


Which is even more interesting and productive, is the fact that "v" and "w" also have 
the maximum at the same point (x,y) on the coordinate plane.


        +-------------------------------------+
        |  It is because  w(x,y) = v^2(x,y).  |
        +-------------------------------------+


Now our task is much more simple: find the point (x,y) on the coordinate plane such that

    x + y = 33600    (1)

and 

    maximizes  w(x,y) = 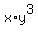,  x >=0,  y >= 0.    (2)


To do it,  from (1)  I express  y = 33600-x  and substitute it into (2).

Then I get the problem to maximize 

    W(x) = .


Apply a standard Calculus procedure: find the derivative and equate it to zero.
You will get then

    (33600-x)^3 = 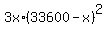,  0 < x < 33600.


Simplify by reducing the factor 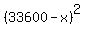  in both sides

    33600-x = 3x

    33600 = 3x + x = 4x

    x = 33600/4 = 8400.


So, the maximum of w(x,y),  v(x,y)  and  u(x,y)  is  achieved at x= 8400,  y= 33600-8400 = 25200

    max u(x,y) = u(8400,25200) = (8400^(1/2)*25200^(3/2)))/400000 = 916.6  (rounded)


ANSWER.  The point of maximum is  (x,y) = (8400,25200).

         The value of the maximum is about 916.6.

         The amount to spend on development is x = $8400,  leaving  $25200 to spend on promotion.