|
Question 1204539: Given the Rational Function f(x)= p(x)/q(x), which of the following statements are true? Check all that apply.
a. If q(x) has a higher degree term than p(x) then the Horizontal Asymptote is y=0
b. If the highest degree term in p(x) is greater than the highest degree term in q(x) there will be more than one Horizontal Asymptote
c. If the highest degree term of p(x) is the same as the highest degree term of q(x) then the Horizontal Asymptote is x=0
d. If f(x) has a HORIZONTAL ASYMPTOTE y=a, then as the input values increase or decrease without bound, the output values will approach a
e. The Horizontal Asymptote is a guiding line for the function as the input values increase or decrease without bound
Found 3 solutions by greenestamps, math_tutor2020, MathLover1:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
a. If q(x) has a higher degree term than p(x) then the Horizontal Asymptote is y=0
TRUE
b. If the highest degree term in p(x) is greater than the highest degree term in q(x) there will be more than one Horizontal Asymptote
FALSE (a) There will be no horizontal asymptote; (b) no function has more than one horizontal asymptote
c. If the highest degree term of p(x) is the same as the highest degree term of q(x) then the Horizontal Asymptote is x=0
FALSE x=0 is not the equation of a horizontal line; and the asymptote is not y=0 either
d. If f(x) has a HORIZONTAL ASYMPTOTE y=a, then as the input values increase or decrease without bound, the output values will approach a
TRUE
e. The Horizontal Asymptote is a guiding line for the function as the input values increase or decrease without bound
TRUE -- assuming a reasonable meaning of "guiding line"
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answers:
(a) True
(b) False
(c) False
(d) True
(e) True
--------------------------------------------------------------
--------------------------------------------------------------
Explanation for part (a)
Let,
n = degree of the numerator
d = degree of the denominator
where degree = largest exponent of a single variable polynomial
If n < d, then this will mean the denominator polynomial races faster to infinity compared to the numerator polynomial.
As such, the denominator gets much larger and the overall fraction approaches 0.
An example would be 
Use a graphing tool such as a TI83, Desmos, or GeoGebra to plot out that equation. You should notice the curve steadily approaches the x axis. It will never actually arrive there.
Or you can use technology to create a table of values to see what happens to the value of y when x gets really large.
For very large values of x, the y values should be really small or 0 depending on how things are rounded. As mentioned, the y value never actually will equal 0 itself.
-------------------------------
Explanation for part (b)
Again we define the following
n = degree of the numerator
d = degree of the denominator
If n = d+1, then we'll have an oblique asymptote or slant asymptote.
An example would be  , in which case the slant asymptote is , in which case the slant asymptote is 
For other cases when n > d+1, the curve's endpoints will approach some other curve.
Meaning the asymptote is no longer a straight line.
Some textbooks would consider the asymptote to be "none", but I think a curve can be an asymptote.
For example,  has its the endpoints approach the cubic curve has its the endpoints approach the cubic curve  . .
This can be determined using polynomial long division or synthetic division.
Synthetic division can be used only when the degree of the denominator is 1.
WolframAlpha can be used to determine the asymptotes.
For example
https://www.wolframalpha.com/input?i=asymptotes+%282x%5E3+%2B+4x%5E2+-+9%29%2F%283+-+x%29
The search input was "asymptotes (2x^3 + 4x^2 - 9)/(3 - x)" without quotes.
The "vertical asymptote" section is basically saying the vertical asymptote is x = 3.
The "parabolic asymptote" section states that 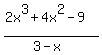 is asymptotic to is asymptotic to 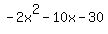
WolframAlpha also provides a graph along with the asymptotes as dashed lines/curves.
-------------------------------
Explanation for part (c)
n = degree of the numerator
d = degree of the denominator
If n = d, then the horizontal asymptote is  where 'a' is the leading coefficient of the numerator, while b is the leading coefficient of the denominator. where 'a' is the leading coefficient of the numerator, while b is the leading coefficient of the denominator.
For example, the horizontal asymptote of  is is 
-------------------------------
Explanation for part (d)
This statement is true.
It can be rephrased to "as x goes to positive or negative infinity, the value of y gets closer to 'a'"
-------------------------------
Explanation for part (e)
The wording "guiding line" is a bit strange, but I'm assuming it refers to the idea the curve steadily approaches this line as x gets really big or really small.
For some rational functions, the curve will cross over the horizontal asymptote. Perhaps more than once. Other rational functions will not have the curve ever touch the horizontal asymptote at all.
For either case, as x goes off to infinity, the curve gets closer to this line.
Further Reading
https://www.mathsisfun.com/algebra/asymptote.html
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given the Rational Function f(x)= p(x)/q(x), which of the following statements are true? Check all that apply.
Asymptotes
A vertical asymptote of a graph is a vertical line x = a where the graph tends toward positive or negative infinity as the inputs approach a.
recall:
If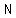 is the degree of the numerator and is the degree of the numerator and 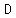 is the degree of the denominator, and is the degree of the denominator, and
if 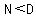 , then the horizontal asymptote is , then the horizontal asymptote is 
if  , then the horizontal asymptote is , then the horizontal asymptote is  = ratio of the leading coefficients. = ratio of the leading coefficients.
if 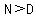 , then there is , then there is  horizontal asymptote. horizontal asymptote.
if  ( the degree of numerator is ( the degree of numerator is  more than the degree of the denominator) ,then there is slant asymptote more than the degree of the denominator) ,then there is slant asymptote
A horizontal asymptote of a graph is a horizontal line  where the graph approaches the line as the inputs approach where the graph approaches the line as the inputs approach  or or  . .
A slant asymptote of a graph is a slanted line  where the graph approaches the line as the inputs approach where the graph approaches the line as the inputs approach  or or  . .
a. If q(x) has a higher degree term than p(x) then the Horizontal Asymptote is y=0
True
reason:
if 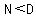 , then the horizontal asymptote is , then the horizontal asymptote is 
b. If the highest degree term in p(x) is greater than the highest degree term in q(x) there will be more than one Horizontal Asymptote
False
reason:
if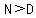 , then there is , then there is 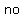 horizontal asymptote. horizontal asymptote.
c. If the highest degree term of p(x) is the same as the highest degree term of q(x) then the Horizontal Asymptote is x=0
False
reason:
if  , then the horizontal asymptote is , then the horizontal asymptote is  = ratio of leading coefficients = ratio of leading coefficients
d. If f(x) has a HORIZONTAL ASYMPTOTE y=a, then as the input values increase or decrease without bound, the output values will approach a.
True
example
 horizontal asymptote of horizontal asymptote of 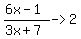 as as  -> ± -> ± 
e. The Horizontal Asymptote is a guiding line for the function as the input values increase or decrease without bound
True
|
|
|
| |