Question 1204529: Radium-221 has a half-life of 30 seconds. How long will it take for 81% of a sample to decay?
Answer by ikleyn(52817)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Radium-221 has a half-life of 30 seconds. How long will it take for 81% of a sample to decay?
~~~~~~~~~~~~~~~~~~~~~~~~
Radium-221 has a half-life of 30 seconds.
Mathematically, it mean M(t) =  ,
where M(t) is the current remaining mass, ,
where M(t) is the current remaining mass, 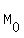 is the initial mass, t is the time, in seconds.
They want you find the time when 81% of the initial uranium isotope will decay;
hence, 19%, or 0.19 of the initial mass remains.
For it, you write the decay equation in terms of half-life
0.19 = is the initial mass, t is the time, in seconds.
They want you find the time when 81% of the initial uranium isotope will decay;
hence, 19%, or 0.19 of the initial mass remains.
For it, you write the decay equation in terms of half-life
0.19 = 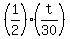 .
Take logarithm base 10 of both sides
log(0.19) = .
Take logarithm base 10 of both sides
log(0.19) =  ,
t = ,
t = 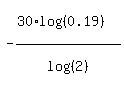 = 71.9 seconds (rounded). ANSWER = 71.9 seconds (rounded). ANSWER
Solved.
--------------------
On radioactive decay, see the lesson
- Radioactive decay problems
in this site.
You will find many similar (and different) solved problems there.
Use this lesson as your handbook, textbook, guide, tutorials, and (free of charge) home teacher.
Learn the subject from there once and for all.
|
|
|