Question 1204452: Suppose that the number of bacteria in a certain population increases according to a continuous exponential growth model. A sample of 2600 bacteria selected from this population reached the size of 2685 bacteria in one and a half hours. Find the hourly growth rate paramete
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose that the number of bacteria in a certain population increases according
to a continuous exponential growth model. A sample of 2600 bacteria selected
from this population reached the size of 2685 bacteria in one and a half hours.
Find the hourly growth rate paramete
~~~~~~~~~~~~~~~~~~~~~~~~
The exponential growth model is
N = 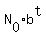 , ,
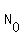 is the initial population size, t is the time, "b" is the base of the exponential function.
For your problem, is the initial population size, t is the time, "b" is the base of the exponential function.
For your problem, 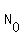 = 2600, t= 1.5 hours, N= 2685, so the equation takes the form
2685 = = 2600, t= 1.5 hours, N= 2685, so the equation takes the form
2685 = 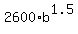 .
Only base "b" is an unknown. To find b, make these standard manipulations, step by step .
Only base "b" is an unknown. To find b, make these standard manipulations, step by step
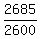 = = 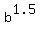 1.032692308 =
1.032692308 = 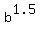 log(1.032692308) = 1.5*log(b)
log(b) =
log(1.032692308) = 1.5*log(b)
log(b) =  = 0.009313961
b = = 0.009313961
b = 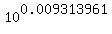 = 1.021677811
ANSWER. The base, or the exponential hourly rate of growth in this problem is 1.021677811.
You may round it to 1.00931, for example. = 1.021677811
ANSWER. The base, or the exponential hourly rate of growth in this problem is 1.021677811.
You may round it to 1.00931, for example.
Solved.
|
|
|