Question 1204418: Find the area of the parallelogram with the following vertices:
1. (-2, 3), (5, 8), (3, 3), and (0, 8)
A. 16 sq units
B. 20 sq units
C. 34 sq units
D. 18 sq units
E. 25 sq units
F. 36 sq units
2. (-2, 7), (-4, 4), (-11, 4), and (-9, 7)
A. 15 sq units
B. 63 sq units
C. 28 sq units
D. 21 sq units
E. 36 sq units
F. 14 sq units
3. (-6, 6), (-6, 3), (-12, 3), and (-12, 6)
A. 36 sq units
B. 54 sq units
C. 15 sq units
D. -45 sq units
E. 18 sq units
F. 24 sq units
4. (12, -3), (5, -6), (5, -3), and (12, -6)
A. 21 sq units
B. -17 sq units
C. 50 sq units
D. 32.5 sq units
E. 42 sq units
F. 30 sq units´
5. (-2, 2), (-6, 9), (-13, 9), and (-9, 2)
A. 10 sq units
B. 25 sq units
C. -55 sq units
D. 64 sq units
E. 35 sq units
F. 49 sq units
Found 3 solutions by erinonimus, greenestamps, math_tutor2020:
Answer by erinonimus(2)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. (-2, 3), (5, 8), (3, 3), and (0, 8)
Let
A (-2,3)
B (5,8)
C (3,3)
D (0,8)
Area of parallelogram = (b1−a1)(d2−a2)−(b2−a2)(d1−a1)
Therefore,
=(5-(-2))(8-3)-(8-3)(0-(-2))
=(5+2)(8-3)-(8-3)(0+2)
=(7)(5)-(5)(2)
=35-10
=25 sq. units
E. 25 sq units
Apply the same formula to the rest of the questions
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The response from the other tutor says to use a magical formula for the area of a parallelogram in terms of the coordinates of the vertices.
That is a good method if all you want to do is to get the answers without learning anything.
In every one of these examples, one pair of sides is either horizontal or vertical, so you can find the area in each case using the basic formula,
Area = base * height
I will get you started on a couple of your examples.
2. (-2, 7), (-4, 4), (-11, 4), and (-9, 7)
(-2,7) and (-9,7) determine a horizontal segment of length 7; (-4,4) and (-11,4) determine another horizontal segment of length 7. The vertical distance between those two horizontal segments is the difference between 4 and 7, which is 3. So the area is 7*3 = 21.
3. (-6, 6), (-6, 3), (-12, 3), and (-12, 6)
(-6,6) and (-6,3) determine a vertical segment of length 3; (-12,3) and (-12,6) determine another vertical segment of length 3. The horizontal distance between those two vertical segments is the difference between -6 and -12, which is -6. So the area is 3*6 = 18. Note that this parallelogram is in fact a rectangle.
Work the other examples by the same process.
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Please post one problem at a time.
I'll focus on problem 1 only.
I'll reorder the points from
(-2, 3), (5, 8), (3, 3), and (0, 8)
to
(-2, 3), (3, 3), (5, 8), and (0, 8)
and I'll give those points the labels A,B,C,D.
A = (-2,3)
B = (3,3)
C = (5,8)
D = (0,8)
Plot those points on the xy plane.
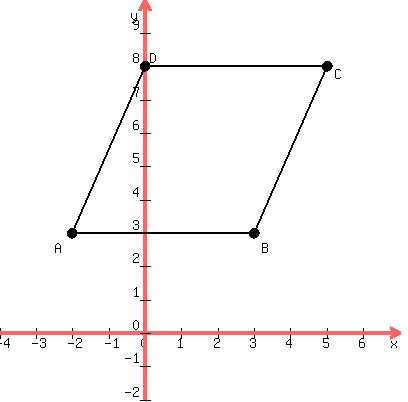
Because points A and B share the same y coordinate, it indicates segment AB is horizontal.
The horizontal segment allows us to quickly compute the segment length.
Segment AB = 5 units long because it's the distance from -2 to 3 on the number line.
Count out the spaces. Alternatively subtract x coordinates and use absolute value.
AB = 5 is the base.
The vertical distance from A(-2,3) to C(5,8) is 5 units because we subtract y coordinates: 8-3 = 5
This represents the height of the parallelogram.
Keep in mind the base and height are always perpendicular to each other.
Then,
area = base*height
area = 5*5
area = 25 square units
The final answer to problem 1 is 25 square units.
-----------------------------------------
Another method
I'll use something called the shoelace formula.
The naming comes from the idea we form a shoelace pattern as shown in the diagram here

Image Source
https://en.wikipedia.org/wiki/Shoelace_formula
Here are alternative names for it:
Gauss's area formula
Surveyor's formula
It appears that tutor @erinonimus is using some variation of this formula.
To set things up, place the coordinates of A through D in four rows like this
A = (-2,3)
B = (3,3)
C = (5,8)
D = (0,8)
Let's delete the labels
(-2,3)
(3,3)
(5,8)
(0,8)
Afterward, we make a copy of the first point (-2,3) and place it at the bottom of the list
(-2,3)
(3,3)
(5,8)
(0,8)
(-2,3)
This will help the list form a loop.
Let's space out the x and y coordinates

After that is set up, draw the diagonals shown here

We multiply along the red diagonal pairs and add up those products
-2*3+3*8+5*8+0*3 = -6+24+40+0 = 58
Do the same for the blue diagonal pairs as well
-2*8+0*8+5*3+3*3 = -16+0+15+9 = 8
Subtract the results
58 - 8 = 50
If this result was negative, then we'd take the absolute value of it to ensure it's positive.
Lastly, take half of this to get the area = (1/2)*50 = 25
The final answer to problem 1 is 25 square units.
A word of caution:
If you swap the positions of B and C, then the shoelace formula will yield an area of 0.
It's a strangely fascinating situation where one half of the area cancels out with the other half (it forms a bow-tie shaped figure).

vs

-----------------------------------------
Some more practice
https://www.algebra.com/algebra/homework/Points-lines-and-rays/Points-lines-and-rays.faq.question.1197252.html
|
|
|