SOLUTION: Find the general solutions (in radians) of the following equations: (a) 3 cot (3𝑥 +𝜋/4) = √3 (b) cos(4𝑥) − 3 sin (3𝜋/2+ 2𝑥) + 2 = 0

Algebra ->  Trigonometry-basics -> SOLUTION: Find the general solutions (in radians) of the following equations: (a) 3 cot (3𝑥 +𝜋/4) = √3 (b) cos(4𝑥) − 3 sin (3𝜋/2+ 2𝑥) + 2 = 0      Log On


   

Question 1204329: Find the general solutions (in radians) of the following equations:
(a) 3 cot (3𝑥 +𝜋/4) = √3
(b) cos(4𝑥) − 3 sin (3𝜋/2+ 2𝑥) + 2 = 0
Answer by ikleyn(52921) About Me  (Show Source):
You can put this solution on YOUR website!
.
Find the general solutions (in radians) of the following equations:
(a) 3 cot (3𝑥 +𝜋/4) = √3
(b) cos(4𝑥) − 3 sin (3𝜋/2+ 2𝑥) + 2 = 0
~~~~~~~~~~~~~~~~~~~~~~~~~~


        In this my post I will solve part  (a),  ONLY. 


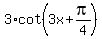    3%2Acot%283x%2Bpi%2F4%29 = sqrt%283%29

implies

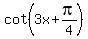    cot%283x%2Bpi%2F4%29 = sqrt%283%29%2F3

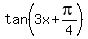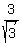
    tan%283x%2Bpi%2F4%29 = 3%2Fsqrt%283%29

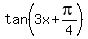    tan%283x%2Bpi%2F4%29 = sqrt%283%29

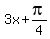    3x%2Bpi%2F4 = p%2F3 + k%2Api,  k = 0, +/-1, +/-2, . . . 


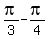    3x = pi%2F3+-+pi%2F4 + k%2Api

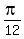    3x = pi%2F12 + k%2Api

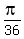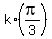    x = pi%2F36 + k%2A%28pi%2F3%29,   k = 0, +/-1, +/-2, . . . 


It is the general solution, in radians.

Solved.

------------------

Do not pack more than one problem per post.