Question 1204310: In how many ways can the number 105 be written as the sum of two or more consecutive positive integers?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! You want  and and  such that such that
 +.....+ +.....+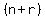
=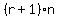 +( +( +.....+ +.....+ ) )
= , ,
which is equivalent to 
.
Notice that, obviously, 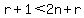 , therefore , therefore  , whence , whence  , so , so
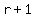 ∈{ ∈{  , , , , , , , , , , , ,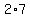 }...(i.e. all the divisors of }...(i.e. all the divisors of  that are ≤ that are ≤ - a total of - a total of  cases). cases).
here they are:
1. If  then then  ; it follows that ; it follows that  and and  , so you have , so you have 
.2 If  then then  ; it follows that ; it follows that  and and  , so you have , so you have 
.
3. If  then 2 then 2 ; it follows that ; it follows that  and and , so you have , so you have 
.
4. If  then then  ; it follows that ; it follows that and and  , so you have , so you have 
.
5 If  then then  ; it follows that ; it follows that  and and  , so you have , so you have

.
6. If  then then  ; it follows that ; it follows that  and and , so you have , so you have 
.
7. If  then then  ; it follows that ; it follows that  and and  , so you have , so you have 
.
Answer by ikleyn(52903)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The "solution" in the post by @MathLover 1 is one-to-one copy-paste from this web-page
https://math.stackexchange.com/questions/2088608/sum-as-an-increasing-sequence-of-two-or-more-consecutive-integers
without any reference, naturally.
|
|
|