Question 120429: Hi! May I have some help with this equation?
Evaluate the expression and write the result in the form a + bi.
1/(4 - 7i)
Found 2 solutions by jim_thompson5910, bucky:
Answer by jim_thompson5910(35256)   (Show Source):
Answer by bucky(2189) (Show Source):
You can put this solution on YOUR website! Given:
.
.
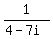
You can convert the denominator of this fraction to a real number by multiplying the denominator
by its conjugate ... the same term as the denominator only with the opposite sign between the
terms. In this case, the conjugate is  . If you multiply the denominator by its
conjugate, you must also multiply the numerator by the same conjugate.
.
This multiplication leads to:
.
.
When you multiply the denominators:
.
.
You can do so by multiplying the 4 in the first set of parentheses by both terms in the second
set of parentheses and then multiplying the -7i from the first set of parentheses by
both terms in the second set of parentheses:
.
.
Notice that the +28i and the -28i are equal but of opposite sign. Therefore, they cancel
each other out and you are left with:
.
.
But, by definition,  . Substitute -1 for  and the expression becomes:
.
.
So the denominator, when multiplied by its conjugate, becomes 65.
.
The numerator, when multiplied by the conjugate, is:
.
.
This numerator is then over the denominator 65 to give:
.
.
So the answer to this problem, in the form a + bi, is:
.
.
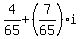
Hope this helps you to understand the problem.
.
|
|
|
