SOLUTION: Assume 𝛼 is opposite side a, 𝛽 is opposite side b, and 𝛾 is opposite side c. Solve the triangle, if possible. Round your answers to the nearest tenth. (If not possible, en

Algebra ->  Trigonometry-basics -> SOLUTION: Assume 𝛼 is opposite side a, 𝛽 is opposite side b, and 𝛾 is opposite side c. Solve the triangle, if possible. Round your answers to the nearest tenth. (If not possible, en      Log On


   

Question 1204286: Assume 𝛼 is opposite side a, 𝛽 is opposite side b, and 𝛾 is opposite side c. Solve the triangle, if possible. Round your answers to the nearest tenth. (If not possible, enter IMPOSSIBLE.)
𝛼 = 36°, 𝛾 = 62°, a = 20
Found 2 solutions by math_tutor2020, MathTherapy:
Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

𝛼 = Greek letter alpha (lowercase)
𝛽 = Greek letter beta (lowercase)
𝛾 = Greek letter gamma (lowercase)

𝛼 = 36°
𝛽 = unknown
𝛾 = 62°

𝛼 + 𝛽 + 𝛾 = 180
36 + 𝛽 + 62 = 180
98 + 𝛽 = 180
𝛽 = 180 - 98
𝛽 = 82°

Sides
a = 20
b = unknown
c = unknown

Angles
𝛼 = 36°
𝛽 = 82°
𝛾 = 62°

Law of Sines
sin(𝛼)/a = sin(𝛽)/b
sin(36)/20 = sin(82)/b
b*sin(36) = 20*sin(82)
b = 20*sin(82)/sin(36)
b = 33.6948933264092 approximately
b = 33.7
Please make sure your calculator is set to degree mode.

Also,
sin(𝛼)/a = sin(𝛾)/c
sin(36)/20 = sin(62)/c
c*sin(36) = 20*sin(62)
c = 20*sin(62)/sin(36)
c = 30.0432033439173 approximately
c = 30.0


The fully solved triangle is
𝛼 = 36°
𝛽 = 82°
𝛾 = 62°
a = 20
b = 33.7
c = 30.0
Diagram

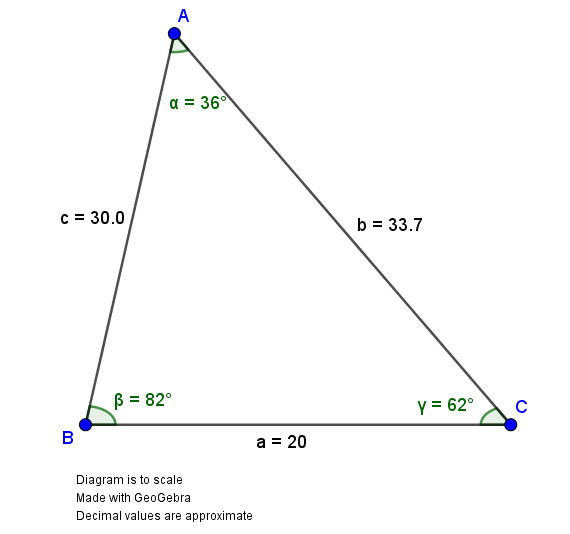
Only one unique triangle is possible due to the AAS congruence theorem.

Answer by MathTherapy(10557) About Me  (Show Source):
You can put this solution on YOUR website!
Assume 𝛼 is opposite side a, 𝛽 is opposite side b, and 𝛾 is opposite side c. Solve the triangle, if possible. Round your answers to the nearest tenth. (If not possible, enter IMPOSSIBLE.)
𝛼 = 36°, 𝛾 = 62°, a = 20

With 𝛼, or ∡A being 36°, 𝛾, or ∡C being 62°, then 𝛽, or ∡B = 82° [180° - (36° + 62°)]

Using the Law of sines, we get: 

Finding side b (opposite 𝛽), we get: matrix%281%2C3%2C+sin+%2836%5Eo%29%2F20%2C+%22=%22%2C+sin+%2882%5Eo%29%2Fb%29
                                 b * sin (36o) = 20 * sin (82o) ---- Cross-multiplying
                                     Side 

Finding side c (opposite 𝛾), we get: matrix%281%2C3%2C+sin+%2836%5Eo%29%2F20%2C+%22=%22%2C+sin+%2862%5Eo%29%2Fc%29
                                 c * sin (36o) = 20 * sin (62o) ---- Cross-multiplying
                                     Side 

Only when 2 sides and one angle are given (SSA or ASS: The famous/infamous DONKEY THEOREM), does the AMBIGUOUS case come into effect. The AMBIGUOUS case involves determining whether ONE or TWO triangles can be formed, based on the given 
information. However, when 2 angles and one side are given (AAS or ASA) - as in THIS CASE - then ONLY ONE (1) triangle
can be formed.