Question 1204285: With each stroke, a pump removes  of the air in a container. After 6 strokes, what is the fraction of the original amount of air in the container that is left? of the air in a container. After 6 strokes, what is the fraction of the original amount of air in the container that is left?
Found 3 solutions by ikleyn, MathLover1, math_tutor2020:
Answer by ikleyn(52848)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
After 1st stroke, 5/6 of the initial air mass remains;
After 2nd stroke, 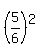 of the initial air mass remains;
After 3rd stroke, of the initial air mass remains;
After 3rd stroke, 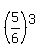 of the initial air mass remains;
After 4th stroke, of the initial air mass remains;
After 4th stroke, 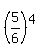 of the initial air mass remains;
After 5th stroke, of the initial air mass remains;
After 5th stroke,  of the initial air mass remains;
After 6th stroke, of the initial air mass remains;
After 6th stroke, 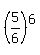 of the initial air mass remains, or 0.3349 of the initial air mass remains (rounded). ANSWER of the initial air mass remains, or 0.3349 of the initial air mass remains (rounded). ANSWER
Solved.
For similar (TWIN) solved problems, see the links
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1097807.html
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.75801.html
at this forum.
///////////////////////
Regarding the post by @MathLover1, I recall this medical proverb:
a drop of nicotine kills a horse.
Likewise, @MatnLover1's answer may kill a reader.
He will die if not from horror to have such a " tutor ", then from laughter.
So, for safety of your mind, you better ignore her post.
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 15625/46656
Which is the same as writing 
How to get that answer:
With one stroke, 1/6 of the air is removed, so 5/6 of the air remains.
Do this 6 times to get (5/6)^6 = (5^6)/(6^6) = 15625/46656
When converting to decimal form,
15625/46656 = 0.3349 = 33.49% approximately
Roughly 33.49% of the original air remains inside the container.
Personally I think a percentage is the best way to represent the final answer, but you should stick to the fraction form since that's what the instructions state.
|
|
|