Question 1204256: Find all rational zeros of the polynomial, and then find the irrational zeros, if any. Whenever appropriate, use the Rational Zeros Theorem, the Upper and Lower Bounds Theorem, Descartes' Rule of Signs, the Quadratic Formula, or other factoring techniques. (Enter your answers as comma-separated lists. Enter all answers including repetitions. If an answer does not exist, enter DNE.)
P(x) = 6x^4 − 11x^3 − 12x^2 + 5x
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52915)   (Show Source):
You can put this solution on YOUR website! .
Find all rational zeros of the polynomial, and then find the irrational zeros, if any.
Whenever appropriate, use the Rational Zeros Theorem, the Upper and Lower Bounds Theorem,
Descartes' Rule of Signs, the Quadratic Formula, or other factoring techniques.
(Enter your answers as comma-separated lists. Enter all answers including repetitions.
If an answer does not exist, enter DNE.)
P(x) = 6x^4 − 11x^3 − 12x^2 + 5x
~~~~~~~~~~~~~~~~~~~~~
Since the constant term is 0 (zero), one root is 0 (zero) - it is obvious
P(x) = 6x^4 - 11x^3 - 12x^2 + 5x = x*(6x^3 - 11x^2 - 12x + 5).
The polynomial of the degree 3 in parentheses has the root x= -1 (according to
the Remainder theorem), since its value at x= -1 is zero
6*(-1)^3 - 11*(-1)^2 - 12*(-1) + 5 = -6 - 11 + 12 + 5 = 0.
So, (x+1) is the divisor for that polynomial. We make this division and get
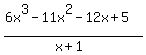 = 6x^2 - 17x + 5.
The quadratic polynomial in the right side (the quotient) has the roots
(use the quadratic formula)
 =  =  ,
 =  =  =  ,
=  =  =  .
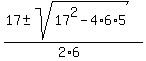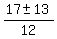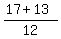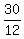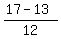ANSWER. The roots of the original polynomial are 0, -1, and .
Solved.
Answer by MathLover1(20850)  (Show Source):
|
|
|
