|
Question 1204250: Let x be a real number such that 625^x=64 Then
125x=a√b. What are a and b?
Found 3 solutions by MathLover1, ikleyn, MathTherapy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let 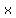 be a real number such that be a real number such that 
Then  What are What are  and and  ? ?
We have the equation 
To simplify the equation, we can express both sides with the same base. We know that  can be expressed as can be expressed as 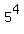 and and  can be expressed as can be expressed as  . .
Rewriting the equation, we have

Using the property of exponents, we can simplify further:

To find  , we need to equate the exponents: , we need to equate the exponents:

Now, solving for : :

Now, we can calculate the value of 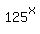 using the value of using the value of 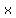 we found: we found:

since  , we have , we have 
then

since  , then , then

so, comparing to  , we have , we have


Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
 , the problem in the post is written incorrectly. , the problem in the post is written incorrectly.
The correct formulation is as follows
Let x be a real number such that 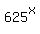 = 64.
Then = 64.
Then 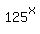 = = 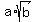 . Find "a" and "b". . Find "a" and "b".
 , the " solution " by @MathLover1 is TOTALLY WRONG. , the " solution " by @MathLover1 is TOTALLY WRONG.
I came to bring a correct solution.
 We are given
We are given 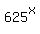 = 64.
It is the same as to write = 64.
It is the same as to write
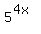 = 64. (1)
Then = 64. (1)
Then
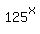 = = 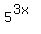 = = 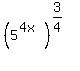 = now replace = now replace 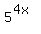 by 64, based on (1) = 64^(3/4) = 8^(3/2) = by 64, based on (1) = 64^(3/4) = 8^(3/2) =  .
Thus the problem is just solved. a = 8; b = 8. ANSWER .
Thus the problem is just solved. a = 8; b = 8. ANSWER
 If 625^x = 64, then x*log(625) = log(64), x =
If 625^x = 64, then x*log(625) = log(64), x =  = 0.646014837 (approximately).
Next, = 0.646014837 (approximately).
Next, 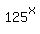 = = 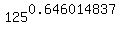 = 22.627417 (approximately); = 22.627417 (approximately);
 = 22.627417 (the same value). Check is completed and confirms the answer. = 22.627417 (the same value). Check is completed and confirms the answer.
Solved.
///////////////////////
For safety of your mind, simply ignore the post by @MathLover1.
Observing her activity at this forum during years, I learned that she DOES NOT know Math, at all
(except of very local pieces).
Her method to work at this forum is to re-write from other tutors or from web-sites
(if she find an appropriate source) - without any reference, naturally.
If she does not find the source to re-write from, she writes any gibberish,
without hesitation.
What others think about her creations, she doesn't care.
Such "tutors" should not be allowed approaching to Math education closer than a cannon shot.
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let x be a real number such that 625^x=64 Then
125x=a√b. What are a and b?
That woman is TOTALLY LOST and CLUELESS!!! Who ever heard of EQUATING the EXPONENTS of 2 exponential expressions when they have DIFFERENT bases?
It appears, as TUTOR @IKLEYN states, that the correct equation is:  .
A different "spin" on this is: .
A different "spin" on this is:  As seen directly above, 2 is being used as the BASE of 64 i/o 8, as Tutor @IKLEYN did. But, 4 could've also been used
since 64 = 43. So, as you may know and can clearly see, 64 can either be expressed as 82, 26, or 43.
As seen directly above, 2 is being used as the BASE of 64 i/o 8, as Tutor @IKLEYN did. But, 4 could've also been used
since 64 = 43. So, as you may know and can clearly see, 64 can either be expressed as 82, 26, or 43.

 ----- EQUATING BASES, since EXPONENTS are the same ----- EQUATING BASES, since EXPONENTS are the same

 -------- --------  As "a" and "b" are being sought from the equation: 125x = a√b, and
As "a" and "b" are being sought from the equation: 125x = a√b, and  , then IN THIS CASE, a = 16, while b = 2
BTW, , then IN THIS CASE, a = 16, while b = 2
BTW,  is the SAME as is the SAME as 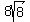 . Check this yourself!! And, if base 4 (43) is used for 64, another set of values for "a" and "b"
- maybe a different set - will ensue! You may want to try that one on your own since 2 of us already used bases 8 and 2. Okay?
Therefore, there is no UNIQUE INTEGER set of values for "a" and "b." . Check this yourself!! And, if base 4 (43) is used for 64, another set of values for "a" and "b"
- maybe a different set - will ensue! You may want to try that one on your own since 2 of us already used bases 8 and 2. Okay?
Therefore, there is no UNIQUE INTEGER set of values for "a" and "b."
|
|
|
| |