Question 1204215: If limt(e^(ln(ax)) × tan(2a/x))= 8 ' find value of a ?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source):
Answer by ikleyn(52812)  (Show Source):
You can put this solution on YOUR website! .
In the post by @MathLover1, this woman made very rude mistakes, which show that
she not only does not know Calculus, but does not know the logarithmic function, as well.
Therefore, I will explain the solution from the very beginning.
If the problem asks about the limit at x---> -oo, then it is clear that the coefficient "a"
in this consideration must be negative - otherwise, logarithm ln(ax) is NOT DEFINED.
With negative "a", ln(ax) is defined at negative x, and we can write 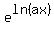 = ax.
Then
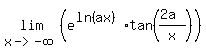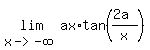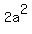 =  =  = 8,
which implies  = 4, and since "a" is negative, a = -2.
So, a = -2 is the only solution to this problem at x ---> -oo, which is exactly opposite to the conclusion by @MathLover1.
If the question is about finding "a" from this equation at x ---> oo, then the answer is a = 2.
Thus, the ANSWER is twofold: if x ---> -oo, then a = -2.
if x ---> oo, then a = 2.
Solved.
---------------
How this woman can call herself " MathLover1 ", making such errors, is a mystery to me.
|
|
|
