Question 1204200: Write the equation of the ellipse that has a center at (5,-4), a vertex at (12,-4), and a covertex at (5,-6).
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52866)   (Show Source):
Answer by MathLover1(20850)  (Show Source):
You can put this solution on YOUR website! The standard form of the equation of an ellipse with center
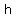( ,  ) and major axis parallel to the  -axis is
where
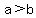
the length of the major axis is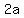 
the coordinates of the vertices are ( ± , )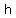
the length of the minor axis is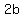
the coordinates of the co-vertices are ( , ± )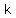
the coordinates of the foci are ( ±  , ), where 
the ellipse that has
a center at ( , )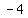
Thus,  , 
vertex at ( ,)=> ( ±  ,)=>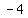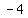
a covertex at (, )=>(,± )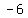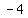
your ellipse is
|
|
|
