Question 1204181: Andrea, a self-employed individual, wishes to accumulate a retirement fund of $200,000. How much should she deposit each month into her retirement account, which pays interest at a rate of 5.5%/year compounded monthly, to reach her goal upon retirement 25 years from now? (Round your answer to the nearest cent.)
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Andrea, a self-employed individual, wishes to accumulate a retirement fund of $200,000.
How much should she deposit each month into her retirement account, which pays interest
at a rate of 5.5%/year compounded monthly, to reach her goal upon retirement 25 years from now?
(Round your answer to the nearest cent.)
~~~~~~~~~~~~~~~~~~~~~~~~~
This problem is posed incorrectly. To be correct, the problem must to point WHEN the deposits
are made, at the end or at the beginning of each compounding period (which is month).
Usually/traditionally, in such problems it is assumed that the deposit are made at the end of each month,
so I will follow this hypothesis. But I should notice, with the DEEP SORROW, that the creators
of this problems do not know the basics of the subject and are not able to pose the problem in a right way.
It is a classic Ordinary Annuity saving plan. The general formula is
FV =  ,
where FV is the future value of the account; P is the monthly payment (deposit); r is the monthly percentage yield
presented as a decimal; n is the number of deposits (= the number of years multiplied by 12, in this case).
From this formula, you get for the monthly payment
P = ,
where FV is the future value of the account; P is the monthly payment (deposit); r is the monthly percentage yield
presented as a decimal; n is the number of deposits (= the number of years multiplied by 12, in this case).
From this formula, you get for the monthly payment
P =  . (1)
Under the given conditions, FV = $200,000; r = 0.055/12; n = 25*12. So, according to the formula (1), you get
for the monthly payment
P = . (1)
Under the given conditions, FV = $200,000; r = 0.055/12; n = 25*12. So, according to the formula (1), you get
for the monthly payment
P = 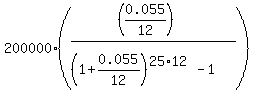 = $311.51.
Answer. The necessary monthly deposit value is $311.51. = $311.51.
Answer. The necessary monthly deposit value is $311.51.
---------
On Ordinary Annuity saving plans, see the lessons
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
in this site.
The lessons contain EVERYTHING you need to know about this subject, in clear and compact form.
When you learn from these lessons, you will be able to do similar calculations in semi-automatic mode.
/////////////////////
To make such complicated calculations as they are in this problem,
you should have/use an appropriate calculator for such long formulas.
Ideal choice is MS Excel, if you have it in your computer.
Then you write a formula in a text editor, copy-paste it
into an Excel work-sheet cell and click "enter" - the result is ready
in the next second.
If you have no MS Excel in your computer, you may find similar
free of charge calculators in the Internet. One such calculator is
www.desmos.com/calculator
It allows you to do the same thing: you write a formula in a text editor,
copy-paste it into this calculator and click "enter" - the result is ready
in the next second.
|
|
|