SOLUTION: An elliptical culvert is 3.2 feet tall and 6.3 feet wide. It is filled with water to a depth of 0.85 feet. Find the width of the stream.

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: An elliptical culvert is 3.2 feet tall and 6.3 feet wide. It is filled with water to a depth of 0.85 feet. Find the width of the stream.      Log On


   

Question 1204151: An elliptical culvert is 3.2 feet tall and 6.3 feet wide. It is filled with water to a depth of 0.85 feet. Find the width of the stream.
Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.
An elliptical culvert is 3.2 feet tall and 6.3 feet wide.
It is filled with water to a depth of 0.85 feet. Find the width of the stream.
~~~~~~~~~~~~~~~~~~~~~~ 

The semiaxes are: 3.2/2 = 1.6 ft long vertical and 6.3/2 = 3.15 ft horizontal.


So, the standard form equation for this ellipse is

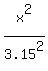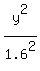    x%5E2%2F3.15%5E2 + y%5E2%2F1.6%5E2 = 1,


written with the center of the ellipse as the beginning of coordinates.


The level of water is at y = -1.6 + 0.85 = -0.75 ft.


Substitute this value of y into the ellipse equation

    x%5E2%2F3.15 + %28-0.75%29%5E2%2F1.6%5E2 = 1,

and get

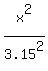    x%5E2%2F3.15%5E2 = 1 - %28-0.75%29%5E2%2F1.6%5E2

or

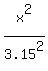    x%5E2%2F3.15%5E2 = 0.780273438.


It implies

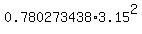    x%5E2 = 0.780273438%2A3.15%5E2 = 7.742263189,

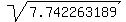    x = sqrt%287.742263189%29 = 2.782492262.


So, the water surface is from x= -2.782492262  to  x= 2.782492262
.


Thus the wide of the stream is  2*2.782492262 = 5.564984524 ft,  or 5.565 ft  (rounded).


ANSWER.  The width of the stream is 5.565 ft,  rounded.

Solved.