Question 1204150: Find the end points of the minor and major axis for the graph of the ellipse
{(x-4)^2/9} + {(y-3)^2/25} = 1
a. Maximum point on the major axis:
b. Minimum point on the major axis:
c. Maximum point on the minor axis:
d. Minimum point on the minor axis:
e. Maximum focal point:
f. Minimum focal point:
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The center is at the point (x,y) = (4,3).
Major semi-axis is of the length of  = 5 from the center vertically.
Minor semi-axis is of the length of = 5 from the center vertically.
Minor semi-axis is of the length of  = 3 from the center horizontally.
So, you just can answer (a), (b), (c), and (d) on your own.
Focal points are at the distance = 3 from the center horizontally.
So, you just can answer (a), (b), (c), and (d) on your own.
Focal points are at the distance  = = 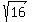 = 4 from the center vertically, up and down.
Having it, you can answer (e) and (f) on your own. = 4 from the center vertically, up and down.
Having it, you can answer (e) and (f) on your own.
Solved.
My congrats (!)
-------------------------
You may learn everything you need from my lesson
- Ellipse definition, canonical equation, characteristic points and elements
in this site in short, clear and compact form.
Do not miss this happy and rare opportunity ( ! )
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! The standard form you need is:

where:

 = the length of the major axis (vertical) = the length of the major axis (vertical)
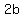 = the length of the minor axis (horizontal) = the length of the minor axis (horizontal)
( , , ) = center of ellipse ) = center of ellipse
you are given:
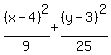
Therefore:
 , , 
 , , 
 , ,
C( , , ) = ( ) = ( , , ) )
The coordinates of the endpoints of the major axis are: ( , , ± ± ) or ( ) or ( , , ), ( ), ( , , ) )
a. Maximum point on the major axis:( , , ) )
b. Minimum point on the major axis:( , , ) )
The coordinates of the endpoints of the minor axis are: ( ± ± , , ) or ( ) or ( , , ), ( ), ( , , ) )
c. Maximum point on the minor axis: ( , , ) )
d. Minimum point on the minor axis: ( , , ) )
e. Maximum focal point:
f. Minimum focal point:
Focal points are at the distance  from the center vertically, up and down from the center vertically, up and down
so, foci are
( , ,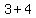 )= ( )= ( , , ) above center ) above center
and
( , ,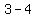 )= ( )= ( , , ) below center ) below center
e. Maximum focal point: ( , , ) )
f. Minimum focal point: ( , , ) )

|
|
|