Question 1204105: When purchasing bulk orders of batteries, a toy manufacturer uses this acceptance sampling plan: Randomly select and test 38 batteries and determine whether each is within specifications. The entire shipment is accepted if at most 3 batteries do not meet specifications. A shipment contains 7000 batteries, and 2% of them do not meet specifications. What is the probability that this whole shipment will be accepted? Will almost all such shipments be accepted, or will many be rejected? The probability that this whole shipment will be accepted is enter your response here.(Round to four decimal places as needed.)
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the probability thqt the whole shipment will be accepted is equal to 0.993131178 this is approximately 99.31% when the percent is rounded to 2 decimal places.
that's the probability that less than or equal to 3 batteries in a sample of 38 batteries will be defective.
the probability that more than 3 batteries will be rejected in a random sample of 38 is equal to 100% - 99.31% = .69%.
i considered this a binomial probability problmm.
the calculations were done in excel.
the formula for each probability is p(x) = p^x * q^(n-x) * c(n,x)
for example, the probability that 3 will be rejected is:
p(3) = .02^3 * .98^(38-3) * c(38,3) = 0.03327662.
that's the same number for p(3) in the spreadsheet.
c(n,x) = n! / (x! * (n-x)!).
that becomes c(38,3) = 38! / (3! * (38-3)!) which is equal to 8436.
this is the same number in the spreadsheet for p(3).
here's the spreadsheet with all the calculations.


Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I'd like to make some comments after the solution by @Theo.
As @Theo shown in his post, the test accepts almost all shipments ($99.31%)
and rejects very few shipments (%0.69).
It means that the test is not adequate and does not perform its functions properly.
It is not surprising.
It is obvious that in order for the test works adequately, it must recognize 2% of the control size.
If three defective batteries are admitted in the shipment, it means that the size of the control set
must be about  = 150 batteries. = 150 batteries.
With the control size of 38 batteries, 3 defective batteries make the gap of 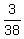 = 0.079 = 7.8%, = 0.079 = 7.8%,
which is too wide and admits (passes) too many defective shipments.
It is what a person, who solves this problem,
should understand after completing the solution.
|
|
|