SOLUTION: People who drink more than 5 drinks in a week are likely to develop cirrhosis of liver 95% of time, whereas people who drink fewer than 5 drinks develop cirrhosis of the liver 20%

    First of all, I want to notice that the problem's formulation is not fully perfect.
    It determines probability for more than 5 drinks and fewer than 5 drinks, 
    but leaves the gap "at 5 drinks".

         So, for correctness, it should be reformulated.

    I modify it this way: "for more than 5 drinks" and "for less or equal 5 drink"
    to fulfill this gap.

In this problem, we have these conditional probabilities given (in shorten form)
(C stands for cirrhosis; ds stands for drinks)


    (a)  P(C | has  >  5 ds ) = 0.95;              

    (b)  P(C | (has <= 5 ds ) = 0.2;

    (c)  P(has > 5 ds) = 0.05   ( which implies  P(has <= 5 ds) = 0.95 ).


They want you find  P(has > 5 drinks | C).



    From (a) we have  P(C and has > 5 ds)  = 0.95*0.05;    (1)

    From (b) we have  P(C and has <= 5 ds) = 0.2*0.95.   (think WHY it is so !)



It implies  P(C) = P(C and has > 5 ds) + P(C and has <= 5 ds) = 0.95*0.05 + 0.2*0.95 = 0.2375.    (2)


        Notice that in (2), I use the modified formulation, which ELIMINATES the gap.


Now the final calculation is  

                              P(C and has > 5 ds)
    P(has > 5 drinks | C)  =  ----------------------- = (from (1) and (2) ) = 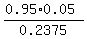 = 0.2  (rounded).    ANSWER 
                                   P(C)