|
Question 1204077: How do you graph the parabola of -12(x+3)=(y-3)^2 that includes the directrix and focus on the graph?
Focus = (-6,3)
Directrix = x=0
Vertex = (-3,3)
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!

Focus = (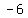 , , ) )
Directrix = 
Vertex = ( , , ) )
Two points determine any line. However, since a parabola is curved, we should find more than two points. In this text, we will determine at least five points as a means to produce an acceptable sketch.
To begin, we graph our first parabola by plotting points. Given a quadratic equation of the form  , , is the independent variable and is the independent variable and  is the dependent variable (so, you choose it). Choose some values for is the dependent variable (so, you choose it). Choose some values for  and then determine the corresponding and then determine the corresponding  -values. Then plot the points and sketch the graph. -values. Then plot the points and sketch the graph.
since you are already given parabola opening sideways and focus is at (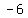 , , ), means the parabola is opening to the ), means the parabola is opening to the  and graph will be in II and III quadrant and graph will be in II and III quadrant
you are also given two points, use them and use formula to find three more
 ...let ...let 

 or or 
 ...let ...let 

 or or 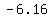
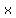 | |
 | |
 | |
 | |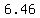
 | |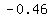
 | |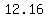
 | |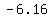
plot these points and sketch the graph

|
|
|
| |