Question 1204036: steve McPoke left home on his bivcycle at 8 am. traveling at 18 km/h. at 10 am, steve's brother set out after him on a motorcycle , folowing the same route. The motorcycle traveled at 54 km/h. How long had steve traveled when his brother overtok him?
Found 4 solutions by MathLover1, ikleyn, math_tutor2020, josgarithmetic:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let's start with the distance formula:
 where where  = distance traveled, = distance traveled,  = rate (speed), and = rate (speed), and  = time of travel. = time of travel.
We can write two such equations, one for Steve (1) and the other for his brother (2):
 ......eq. (1) ......eq. (1)
and
 .......eq.(2) .......eq.(2)
Now when Steve's brother on the motor bike overtakes Steve on his bicycle, each will have traveled the same distance, so:

and, since Steve's brother set out two hours after Steve did (10 am - 8 am), then Steve's time is two hours more than his brother's time, and, of course, the speeds of both are given, so:

Now we have enough information to complete the two equations:


Since  we'll set these two equations equal to each other to get: we'll set these two equations equal to each other to get:
 ........ Solve for ........ Solve for 
 ......... Subtract ......... Subtract 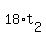 from both sides. from both sides.
 ........Divide both sides by ........Divide both sides by  . .
 but we want Steve's time ( but we want Steve's time ( , so , so
 ....... Substitute ....... Substitute 


Steve had traveled for  hours when his brother overtook him. hours when his brother overtook him.
Answer by ikleyn(52847)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
steve McPoke left home on his bivcycle at 8 am. traveling at 18 km/h.
at 10 am, steve's brother set out after him on a motorcycle , folowing the same route.
The motorcycle traveled at 54 km/h. How long had steve traveled when his brother overtok him?
~~~~~~~~~~~~~~~~~~~~~~
A quick and short "naive" solution
In 2 hours, Steve is 2*18 = 36 kilometers from the home.
Moving faster than Steve, his brother has approaching speed of 54-18 = 36 km/h.
Therefore, it is clear that the brother will overtake Steve in 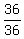 = 1 hour.
So, Steve travels 2+1 = 3 hours when the brother overtakes him. ANSWER = 1 hour.
So, Steve travels 2+1 = 3 hours when the brother overtakes him. ANSWER
A slow Algebra solution
Let t be the time after the brother started.
So, to the catching moment, the brother moves t hours.
Steve started earlier, so Steve moved (t+2) hours till the brother overtook him.
They cover the same distance, so we write this distance equation
54*t = 18*(t+2)
Left side is the distance covered by the brother; right side is the distance covered by Steve.
To solve, simplify the equation. You will get
54t = 18t + 36
Simplify and find t
54tt - 18t = 36
36t = 36
t = 36/36 = 1 hour.
So, the brother overtakes Steve in 1 hour after the brother starts.
Steve travels 2+1 = 3 hours when the brother overtakes him. ANSWER
You get the same answer.
Solved (in two different ways for your better understanding).
----------------
For simple Travel & Distance problems, see introductory lessons
- Travel and Distance problems
- Travel and Distance problems for two bodies moving in opposite directions
- Travel and Distance problems for two bodies moving in the same direction (catching up)
in this site.
They are written specially for you.
You will find the solutions of many similar problems there.
Read them and learn once and for all from these lessons on how to solve simple Travel and Distance problems.
Become an expert in this area.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
n = number of hours that elapse after 8 am.
Steve travels for n hours
Steve travels 18n kilometers because distance = rate*time.
Steve's brother travels n-2 hours because he's on the road for two fewer hours. Eg: Steve is on the road for 5 hours, while his brother is on the road for 3 hours.
Steve's brother travels 54(n-2) kilometers.
Steve's brother catches up to Steve when the two men travel the same distance.
18n = 54(n-2)
18n = 54n-108
18n-54n = -108
-36n = -108
n = -108/(-36)
n = 3
Steve's brother catches up with Steve 3 hours after 8 am.
The two brothers meet up at 11 am because 8 am + 3 hrs = 11 am.
-------------------------------------
Another method
m = number of hours Steve's brother is on the road.
m+2 = number of hours Steve is on the road, since he gets a 2 hour head start.
18(m+2) = distance Steve travels
54m = distance Steve's brother travels
18(m+2) = 54m
18m+36 = 54m
36 = 54m-18m
36 = 36m
36m = 36
m = 36/36
m = 1
Steve's brother is on the road for 1 hour.
The two brothers meet up at 11 am since 10 am + 1 hr = 11 am
Steve is on the road for m+2 = 1+2 = 3 hours when his brother passes him.
-------------------------------------
Answer: 3 hours
Answer by josgarithmetic(39625)   (Show Source): (Show Source):
|
|
|