SOLUTION: In how many ways can a class of 16 students be assigned 2 A's, 6 B's, 3 C's, 2 D's and 3 F's?

Click here to see ALL problems on Probability-and-statistics

Question 1204021: In how many ways can a class of 16 students be assigned 2 A's, 6 B's, 3 C's, 2 D's and 3 F's?

Found 3 solutions by Edwin McCravy, ikleyn, greenestamps:
Answer by Edwin McCravy(20060)   (Show Source):
You can put this solution on YOUR website!

Choose the A students C(16,2)=120 ways.
Choose the B students C(16-2=14,6)=C(14,6)=3003 ways.
Choose the C students C(14-6=8,3)=C(8,3)=56 ways.
Choose the D students C(8-3=5,2)=C(5,2)=10 ways.
Choose the F students C(5-2=3,3)=C(3,3)=1 way.
Answer = (120)(3003)(56)(10)(1) = 201801600
Edwin

Answer by ikleyn(52803)   (Show Source):
You can put this solution on YOUR website!
.

This problem is a TWIN to the problem solved 5 minutes ago

https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1204022.html

The same logic works.

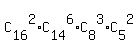= 120 * 3003 * 56 * 10 = 201801600 different ways. ANSWER

Solved.

----------------

To see many similar (and different) problems, solved and explained, look into the lesson
    - Fundamental counting principle problems
in this site.

Learn the subject from there.

Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

In solving a problem like this, it is useful to know that the different grades can be assigned in any order; the result will be the same. For example, if the grades are assigned from lowest (F) to highest (A), then the calculation is

Of course the last factor is not needed -- but showing it makes the complete process more clear.

And a third way to find the answer to the question is to count the number of different ways of arranging the 16 grades in a string:

AABBBBBBCCCDDFFF

By a well-known counting principle, the number of distinct arrangements of those letters is