Question 1203860: suppose you want to have 500,000 for retirement in 20 years your account earns 4% interest how much would you need to deposit in the account each month
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
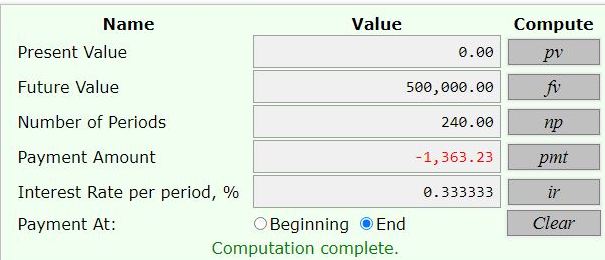
You can put this solution on YOUR website! calculator used is at https://arachnoid.com/finance/
monthly compounding is assumed.
presen value = 0
future value = 500,000
number of time periods = 20 years * 12 = 240 months.
interest rate per time period = 4% per year / 12 = .333333333....% per month.
payments are made at the end of each month.
calculator says that you need to invest 1363.23 at the end of each month so that you can have 500,000 at the end of the investment period.
here are the results from using the calculator.
Answer by ikleyn(52869)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose you want to have 500,000 for retirement in 20 years your account earns 4% interest
how much would you need to deposit in the account each month
~~~~~~~~~~~~~~~~~~~~~~~~~~
This my solution goes second after the solution by @Theo.
@Theo used an online calculator in his solution.
Since this web-site is to teach Math, the expected solution should be mathematical.
So, I present here a standard mathematical solution.
Calculator can be used as a secondary tool for verification.
Then the sequence of steps would be normally educative.
I will assume that the problem is about ordinary annuity saving account,
i.e. depositing and compounding are made at the end of each month.
Use the formula for the Future Value of the ordinary annuity
FV =  ,
where FV is the future value of the account; P is the monthly payment (deposit);
r is the monthly effective compounding rate presented as a decimal;
n is the number of deposits (= the number of years multiplied by 12, in this case).
From this formula, you get for the monthly payment
P = ,
where FV is the future value of the account; P is the monthly payment (deposit);
r is the monthly effective compounding rate presented as a decimal;
n is the number of deposits (= the number of years multiplied by 12, in this case).
From this formula, you get for the monthly payment
P =  . (1)
Under the given conditions, FV = $500,000; r = 0.04/12; n = 20*12.
So, according to the formula (1), you get for the monthly payment value
P = . (1)
Under the given conditions, FV = $500,000; r = 0.04/12; n = 20*12.
So, according to the formula (1), you get for the monthly payment value
P = 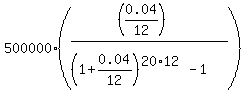 = 1363.25 (rounded to closest greater cent).
It is practically the same value as @Theo obtained in his post using a calculator.
Answer. The necessary monthly deposit value is $1363.25. = 1363.25 (rounded to closest greater cent).
It is practically the same value as @Theo obtained in his post using a calculator.
Answer. The necessary monthly deposit value is $1363.25.
Solved.
---------------------------
In such calculations, it is important to avoid intermediate rounding.
Rounding can be done at the end, only.
Intermediate rounding is PROHIBITED, since it leads to wrong answer.
Also, a calculator should provide the necessary precision.
I use MS Excel in my computer. It works with 15 decimals in mantissa
and provides the necessary precision.
I simply copy-paste my numerical formula into Excel spreadsheet and get the answer in one click.
Many standard online calculators provide the necessary precision.
You may use, for example, these free-of-charge online calculators
https://www.omnicalculator.com/finance/annuity-future-value
https://www.calculatorsoup.com/calculators/financial/future-value-annuity-calculator.php
https://www.calculator.net/future-value-calculator.html
They are reliable, have convenient user-friendly interface, have complete instructions and descriptions,
provide the necessary precision and were checked million times. You may use them to check my/your calculations.
//////////////////////////////////////////
There is another (= one more) reason why I produced and placed my solution here.
@Theo' posts used visual plots to support his solutions.
These plots were integral inseparable part of his solutions.
But some time ago, Theo left this forum and stopped supporting web-site with his plots.
As a result, you see now some colored spots in his posts, where his plots should be.
Due to this reason, @Theo's post lost their educational meaning and value.
Therefore, I create my posts with my own mathematical solutions
to replace @Theo' solutions and provide meaningful mathematical content.
|
|
|