Question 1203820: Find all exact solutions on the interval 0 ≤ x < 2𝜋. (Enter your answers as a comma-separated list.)
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52874)   (Show Source):
You can put this solution on YOUR website! .
Find all exact solutions on the interval 0 ≤ x < 2𝜋. (Enter your answers as a comma-separated list.)
cot(x) + 5 = 6
~~~~~~~~~~~~~~~~~~~
cot(x) + 5 = 6 implies, step by step
cot(x) = 6 - 5
cot(x) = 1
x =  or x =  .
ANSWER. There are two solutions in the given interval: x = or x = .
Solved.
====================
Regarding the solution by @Theo to this problem, notice that the part of his reasoning and calculations
below his plot, where he considers cotan(7) and arctan(1/7), is fully irrelevant to the problem
and is placed there by him for unknown reasons (by mistake ?).
Regarding his other notice that solving equation cot(x) = 1 requires to convert cotangent to equivalent tangent function,
I would be more careful with such statements.
This equation, cot(x) = 1 requires only knowledge of basic notions of Trigonometry
and knowledge of table values of basic trigonometric functions.
In general, this idea by @Theo to use a calculator to solve equation cot(x) = 1
does not seem a productive to me. A student, who is literate in Trigonometry,
should/MUST solve such equation MENTALLY, and it is a right way to teach.
If a student uses a calculator for such purposes, it clearly shows that this student
does not know the basics of Trigonometry. Such a student must re-learn
the basics of Trigonometry from scratch.
So, my impression is that the whole @Theo's post is WRONG TEACHING.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! cot(x) + 5 = 6
subtract 5 from both sides of the equation to get:
cot(x) = 1
since cot(x) = 1/tan(x), you get:
1/tan(x) = 1
solve for tan(x) to get:
tan(x) = 1/1 = 1
if your calculator is set to degrees....
solve for x to get:
arctan(1) = 45 degrees.
tangent is positive in the first and third quadrants.
the equivalent angle in the third quadrant is 180 + 45 = 225 degrees.
in the interval between 0 and 360 degrees, your angle will be 45 degrees and 225 degrees.
here's what it looks like on a graph.
if your calculator is set to radians....
solve for x to get:
arctan(1) = .7853981634 radians.
tangent is positive in the first and third quadrants.
the equivalent angle in the third wuadrant is pi + .7853981634 = 3.926990817 radians.
in the interval between 0 and 2pi radians, your angle will be .7853981634 radians and 3.926990817 radians.
here's what it looks like on a graph.
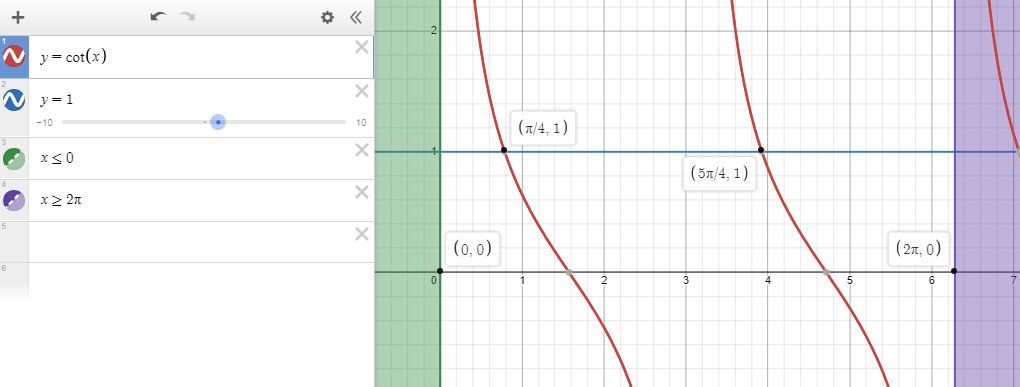
note that .7853981634 radians is equal to .25 * pi radians which is equal to pi/4 radians, as shown on the graph.
note also that 3.926990817 radians is equal to 1.25 * pi radians which is equal to 5pi/4 radians, as shown on the graph.
note that most calculators don't handle cotangent function directly.
my ti-84 plus is one of them.
to solve for cotangent, it is necessary to convert cotangent to equivalent tangent function.
as an example:
if cotan(x) = 7, then 1/tan(x) = 7.
solve for tan(x) to get tan(x) = 1/7.
calculator says that x = arctan(1/7) = 8.130102354 degrees.
that should be your angle.
cot(8.120102354) should be equal to 7.
since cot = 1/tan, then 1/tan(8.120102354) = 7
use your calculator to get 1/tan(8.120102354) = 7.
the graphing software i use (desmos.com) can handle cotangent function directly, as you can see.
|
|
|
