|
Question 1203788: Find the point (𝑥,𝑦) on the line 𝑦=−2𝑥+4
that is equidistant from the points (8,−3) and (−5,−10)
Found 3 solutions by josgarithmetic, MathLover1, greenestamps:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! given:
the points ( , , ) and ( ) and (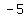 , ,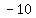 ) )
 .........eq.1 .........eq.1
using distance formula
distance from ( , , ) to ( ) to ( , , ) is equal to distance from ( ) is equal to distance from ( , , ) to ( ) to ( , , ) )


 .........eq. 2 .........eq. 2
equal eq.1 and eq.2
 ....solve for ....solve for 

plug in  ----eq.1 ----eq.1


so, point is
( , , )=( )=( , ,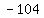 ) )
check: if the distances of ( , ,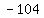 ) from ( ) from ( , , ) and ( ) and ( , , ) are same ) are same
the distances of ( , ,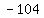 ) from ( ) from ( , , ) is ) is  ≈ ≈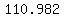
the distances of ( , ,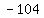 ) from ( ) from ( , , ) )
is  ≈ ≈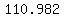
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If the distances are the same, then the squares of the differences are the same. So in doing the calculations, we don't need to bother with the"square root" part of the distance formula.
The two given points are (8,-3) and (-5,-10); the point we are looking for is (x,-2x+4).
The square of the distance from one of the given points to the unknown point is equal to the square of the distance from the other given point to the unknown point:





The point we are looking for is (x,-2x+4) = (54,-104)
ANSWER: (54,-104)
CHECK (verify that the square of the distance from (8,-3) to (54,-104) and the square of the distance from (-5,-10) to (54,-104) are equal):
(54-8)^2+(-104+3)^2 = 46^2+101^2 = 12317
(54+5)^2+(-104+10)^2 = 59^2+94^2 = 12317
|
|
|
| |