Question 1203785: I'm so confused on what my math teacher is asking...
Sin θ=4/5, cos θ=-3/5
I need to find θ but I don't understand how to solve for it. If you could show me how to do it or maybe even if possible show me some examples it would be greatly appreciated because I really want to try and solve the rest of the problems myself. :D
Found 4 solutions by MathLover1, math_tutor2020, ikleyn, mccravyedwin:
Answer by MathLover1(20849)   (Show Source):
Answer by math_tutor2020(3816)  (Show Source):
You can put this solution on YOUR website!
sin(θ) = 4/5
θ = arcsin(4/5) or θ = 180 - arcsin(4/5)
θ = 53.1301° or θ = 126.8699°
Both are approximate.
Arcsine refers to inverse sine, denoted on many calculators as the button 
Take note how sin(53.1301°) = 4/5 = 0.8 approximately and also sin(126.8699°) = 4/5 = 0.8 approximately as well.
The answer we want is either θ = 53.1301° or θ = 126.8699°
Which one do we pick? We go for the one that makes cosine negative.
cos(53.1301°) = 0.6 = 3/5
cos(126.8699°) = -0.6 = -3/5
Therefore, θ = 126.8699° approximately
To convert to radians, multiply by the conversion factor pi/180.
This would mean:
126.8699° = 126.8699*(pi/180) = 2.2143 radians approximately
In my opinion, degrees are easier to work with in this context.
Side note: The angle 126.8699° is in quadrant 2, aka the northwest quadrant.
Answer by ikleyn(52775)  (Show Source):
You can put this solution on YOUR website! .
@MathLover1 incorrectly interprets the problem as two separate cases,
giving two separate answers.
So you, the reader, may get confused.
See the correct interpretation and correct ( !  ! ) answer in the post by @math_tutor2020.
Answer by mccravyedwin(406)  (Show Source):
You can put this solution on YOUR website!  , 
You should memorize which trig ratios are positive and which ones are
negative in which quadrants.
In QI, ALL 6 trig ratios are positive.
In QII, Only the SINE and its reciprocal, the cosecant, are positive and the other 4 are negative.
In QIII, Only the TANGENT and its reciprocal, the cotangent, are positive and the other 4 are negative.
In QIV, Only the CALCULUS and its reciprocal, the secant, are positive and the other 4 are negative.
An easy mnemonic way to memorize this is to memorize this sentence for the
basic 3 trig functions sine, cosine, and tangent.
ALL STUDENTS TAKE CALCULUS.
Back to your problem:
,
The sine, 4/5, is a POSITIVE number, so if you've memorized the above, you
know that the sine is only positive in QI and QII
The cosine, -3/5 is a NEGATIVE number, so if you've memorized the above, you
know that the cosine is only positive in QI and QIV, so it is negative only in QII and QIII.
Therefore we know that θ is in QII. So we draw a right triangle in QII,
with one side on the x axis. Angles are always measured counter-clockwise from
the right side of the x-axis. So we draw an arc to indicate the angle θ.
The x value is the adjacent side, the y-value is the opposite side, the r-value is the hypotenuse.
Angle θ is OUTSIDE the triangle and the reference angle is INSIDE the
triangle, indicated in green by ref(θ). We use only positive numbers to
calculate the reference angle.
We find the value of the reference angle by calculator using ONLY POSITIVE
NUMBERS. The sine of the reference angle is its opposite 4, over the
hypotenuse 5. So on the TI-84, in degree mode, we press
2nd, sin, 4, ÷, 5,
We see this:
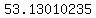So the reference angle is 53.13010235o.
The actual angle is measured by the red arc, so we subtract that value
from 180o, and get 126.8698977o.
126.8698977o <--answer
Edwin
|
|
|
