Question 1203784: Sketch two periods of the graph for the following function.
f(x) = 5sec(3x)
Identify the stretching factor and period.
Identify the asymptotes in the displayed domain of the graph you selected above. (Enter your answers as a comma-separated list of equations.)
Found 3 solutions by MathLover1, Theo, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! euation is f(x) = 5sec(3x)
general form is f(x) = a * sec(b * (x-c)) + d
a is the amplitude.
b is the frequency.
c is the horizontal shift.
d is the vertical shift.
i believe they are referring to the amplitude as the stretching factor.
the default is 1 unit above and 1 unit below the center horizontal line.
when it is 5, the amplitude is 5 times as much above and below the horizontal line.
the normal period of the secant function is 360 degrees.
the freuency for the secant function is equal to 360 / the period.
the period for the secant function is equal to 360 / the frequency.
the frequency for this secant function is 3.
the period is therefore 360 / 3 = 120 degrees.
there is no horizontal shift.
here is no vertical shift.
the graph of this runction is shown below.

the secant function is in red.
the cosine function is in blue.
you want the secant function.
i only showed the cosine function because the secant function is equal to 1 divided by the cosine function.
i thought it would be easier for you to see that it is the reciprocal of the cosine function that way.
the graph that you want is the red graph.
the asymptotes are at 0 degrees and at 120 degrees.
that's where the cosine function = 0.
since the secant function is 1 / cosine function, that's where the secant function is undefined.
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Sketch two periods of the graph for the following function.
f(x) = 5 sec(3x)
Identify the stretching factor and period.
Identify the asymptotes in the displayed domain of the graph you selected above.
(Enter your answers as a comma-separated list of equations.)
~~~~~~~~~~~~~~~~~~~~~~~~
Teaching by @MathLover1 in her post is INCORRECT and WRONG.
Many of her numbers are wrong; her argumentation is defective; her explanations are incorrect.
@Theo uses inappropriate terminology/terms as " amplitude ", " frequency ", that are used
for harmonic sinusoidal functions ONLY, so if you will use it, you may find yourself
in unpleasant situation, when everybody around will look at you with squared eyes.
In addition, @Theo in his post makes a RUDE MISTAKE, stating that the given function
has vertical asymptotes at x= 0 degrees and x= 120 degrees. The asymptotes are different - see my post.
I came to bring correct answers to posed questions and to make this job in a way as it should be done.
And using ( it is IMPORTANT ! ) right words, connected in right order into right sequence
for readers to use my post as a universal mantra.
(1) To sketch the plot, go to web-site www.desmos.com/calculator
Find there free of charge plotting tool for common use.
Print the equation of the function and get the plot in the next instance.
(2) In this problem, there are 2 (two) stretching factors: one vertical and one horizontal,
and both deserves to be discussed.
Vertical stretching factor is 5. It is the coefficient (multiplier) before the function "sec".
In this problem, this coefficient is greater than 1, so it really produces vertical stretching
with coefficient 5.
Horizontal stretching coefficient is 1/3, and because it is less than 1, in this problem
it is better to speak about horizontal compression with coefficient 3.
The period is  .
(3) Since 5sec(3x) = .
(3) Since 5sec(3x) = 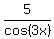 , vertical asymptotes are where cos(3x) is zero.
cos(3x) is zero where 3x = , vertical asymptotes are where cos(3x) is zero.
cos(3x) is zero where 3x =  , or at x= , or at x= 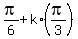 , k= 0, +/-1, +/-2, . . .
So, vertical asymptotes are at x= , k= 0, +/-1, +/-2, . . .
So, vertical asymptotes are at x= 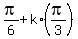 , k= 0, +/-1, +/-2, . . .
First two vertical asymptotes in positive domain are at x= , k= 0, +/-1, +/-2, . . .
First two vertical asymptotes in positive domain are at x= 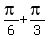 = = 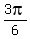 = = 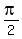 and x= and x= 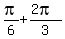 = =  . .
Solved and answered in correct form, as it should be done,
with explanations where necessary.
|
|
|