.
Let P(E) = 0.45, P(F) = 0.55, and P(F ∩ E) = 0.25. Draw a Venn diagram and find the conditional probabilities.
(a) P(E | F^C )
(b) P(F | E^C )
~~~~~~~~~~~~~~~~~~~~~~~~~
(a) Conditional probability P(E | F^C ) is
P(E | F^C ) =  The intersection E_and_F^c consists of those elements of E that do not belong to F.
Hence, the set E_and_F^c is the same as E \ (E ∩ F).
Therefore, P(E_and_F^c) = P(E) - P(E ∩ F) = 0.45 - 0.25 = 0.2.
From the other side, P(F^c) = 1-P(F^c) = 1 - P(F) = 1 - 0.55 = 0.45.
Thus P(E | F^C ) =
The intersection E_and_F^c consists of those elements of E that do not belong to F.
Hence, the set E_and_F^c is the same as E \ (E ∩ F).
Therefore, P(E_and_F^c) = P(E) - P(E ∩ F) = 0.45 - 0.25 = 0.2.
From the other side, P(F^c) = 1-P(F^c) = 1 - P(F) = 1 - 0.55 = 0.45.
Thus P(E | F^C ) =  =
= 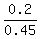 =
=  =
=  . ANSWER
. ANSWER
The solution for (b) follows the same logic.
(b) The answer for (b) is  =
=  =
= 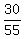 =
=  .
.
Solved.