Question 1203748: Please help me with this calculus problem about derivatives of Inverse functions.

picture hosting
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Calculate g(b) and g'(b) where g is the inverse function of f(x).
f(x) = x + sin(x), b= 1.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
You are given function f(x) = x + sin(x).
They want you find g(1), where g(x) is the inverse function of f(x).
First of all, in order you understand better everything from the very beginning,
f(x) = x + sin(x) is a MONOTONIC function on the entire domain, which is the set of all real numbers.
The range of f(x) is the entire set of real numbers.
It is monotonic function, since its derivative f'(x) = 1 + cos(x) is non-negative everywhere
excluding discrete points x =  , k = 0, +/-1, +/-2, . . .
g(1) is the real number x such that f(x) = x + sin(x) = 1. (1)
Since f(x) is monotonic, such number x (the root of the equation (1),
(a) exists, and
(b) is UNIQUE.
To find this root x, the algebraic methods do not work. We should use numerical methods
and special computer solvers.
One such solver is Wolfram Mathworld / Transcendent solver
https://mathworld.wolfram.com/TranscendentalEquation.html
It is free of charge.
Using it, we find the root of equation (1). It is x = 0.510973.
So, g(1) = 0.510973 (approximate value).
Now we should find g'(1).
Use the identity for inverse function g'(b) = 1/f'(x). It gives
g'(1) = 1/f'(0.510973) = , k = 0, +/-1, +/-2, . . .
g(1) is the real number x such that f(x) = x + sin(x) = 1. (1)
Since f(x) is monotonic, such number x (the root of the equation (1),
(a) exists, and
(b) is UNIQUE.
To find this root x, the algebraic methods do not work. We should use numerical methods
and special computer solvers.
One such solver is Wolfram Mathworld / Transcendent solver
https://mathworld.wolfram.com/TranscendentalEquation.html
It is free of charge.
Using it, we find the root of equation (1). It is x = 0.510973.
So, g(1) = 0.510973 (approximate value).
Now we should find g'(1).
Use the identity for inverse function g'(b) = 1/f'(x). It gives
g'(1) = 1/f'(0.510973) = 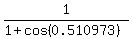 = = 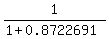 = 0.534111 (approximate value).
ANSWER. g(1) = 0.510973 (approximate value). g'(1) = 0.534111 (approximate value). = 0.534111 (approximate value).
ANSWER. g(1) = 0.510973 (approximate value). g'(1) = 0.534111 (approximate value).
The problem is solved, in full,
with complete explanations.
=====================
Ignore the post by @MathLover1, for your safety,
since madam simply doesn't know the subject.
////////////////////
In order for your understanding would be even better,
I advise you to go to web-site www.desmos.com/calculator
Find there free of charge plotting tool and make plots of functions
f(x) = x + sin(x) and h(x) = 1.
You will see monotonicity of f(x) and will see the root of equation f(x) = 1,
where the intersection point of these two plots is.
|
|
|