|
Question 1203719: Create an equation of a piecewise function that has the following properties:
- includes 4 different types of functions (e.g. linear, quadratic, exponential, square root)
- is continuous
- has limiting behaviour as x --> ± ∞, y --> + ∞
Found 3 solutions by Edwin McCravy, greenestamps, mccravyedwin:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! Create an equation of a piecewise function that has the following properties:
- includes 4 different types of functions (e.g. linear, quadratic, exponential, square root)
- is continuous
- has limiting behaviour as x --> ± ∞, y --> + ∞

 must be a line through must be a line through 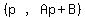 ,
and its slope A must be negative since it must approach +∞ as x approaches -∞.
So the line must rise to the left and drop to the right. Lines that do this have
negative slopes.
You must find values for A,...,I and p,q,r, where p < q < r so that each part
connects to the next. Maybe you can choose some of those to be 0. But not
A,C,F,H. Maybe you can choose at least some of them to be 1 or -1.
I'll work on it some more. This is quite a problem!
Edwin ,
and its slope A must be negative since it must approach +∞ as x approaches -∞.
So the line must rise to the left and drop to the right. Lines that do this have
negative slopes.
You must find values for A,...,I and p,q,r, where p < q < r so that each part
connects to the next. Maybe you can choose some of those to be 0. But not
A,C,F,H. Maybe you can choose at least some of them to be 1 or -1.
I'll work on it some more. This is quite a problem!
Edwin
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Assuming the four types of equations are in fact linear, quadratic, exponential, and square root....
(1) exponential and square root functions are monotonically increasing where they are defined. Since the behavior must be y goes to infinity as x goes to negative infinity, the leftmost part of the graph must be either linear (with a negative slope) or quadratic.
(2) a linear equation is probably the easiest to fit with the other types of functions, so let's not start with a linear function. So we will make the leftmost part of the graph quadratic.  is a simple one to work with. is a simple one to work with.
(3) (1,1) is a solution to both  and and  , so it looks as if making the second function equal to , so it looks as if making the second function equal to  will be convenient. We can stop using that function at a convenient point, say (4,2). will be convenient. We can stop using that function at a convenient point, say (4,2).
(4) Making the third function linear will make it easy to make the "junction" between it and the fourth (exponential) function continuous. So choose a simple linear function containing (4,2):  . We can end it again at a convenient point, say (5,3). . We can end it again at a convenient point, say (5,3).
(5) Then the fourth function is exponential containing (5,3). Although it doesn't look "nice", the function  will do the job. will do the job.
One of an infinite number of possibilities....
 for x less than 1 [red in the graph below] for x less than 1 [red in the graph below]
 for x greater than or equal to 1 and less than 4 [green] for x greater than or equal to 1 and less than 4 [green]
 for x greater than or equal to 4 and less than 5 [blue] for x greater than or equal to 4 and less than 5 [blue]
 for x greater than or equal to 5 [purple] for x greater than or equal to 5 [purple]
Here is a graph with the four functions overlapping, and showing the piecewise graph continuous at (1,1), (4,2), and (5,3):

Answer by mccravyedwin(407)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Greenestamps has found an answer. This is his piecewise function:
 I'll draw the final graph of his answer.
Notice that his last part looks like a vertical line, but it is NOT!!
It is a very rapidly increasing exponential function. It increases
from (5,3) way up to the point (6,258+) and all the way to +infinity.
I'll draw the final graph of his answer.
Notice that his last part looks like a vertical line, but it is NOT!!
It is a very rapidly increasing exponential function. It increases
from (5,3) way up to the point (6,258+) and all the way to +infinity.
 Edwin
Edwin
|
|
|
| |