|
Question 1203711: A movie theater has a seating capacity of 367. The theater charges $5.00 for children, $7.00 for students, and the $12.00 for adults. There are half as many adults as there are children if the total tickets sales was $2668, how many children, students, and adults attended?
Found 4 solutions by mananth, greenestamps, ikleyn, josgarithmetic:
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! The theater charges $5.00 for children,
Let there be x children
$7.00 for students,
Let there be y students
and the $12.00 for adults.
Number of adults will be x/2
A movie theater has a seating capacity of 367.
x+x/2+y =367
multip;y by LCD 2
2x+x+2y = 734
3x+2y = 734------------1
the total tickets sales was $2668
5x+7y+12*(x/2)=2668
11x+7y = 2668-------------2
Multiply (!) by 11 and (2) by 3 and subtract
33x+22y=8074
33x +21y = 8004
y = 70
Plug y =70 in (1)
3x+2y = 734
3x+140 = 734
3x = 734-140= 594
x = 198
x/2 = 99 (Adults)
x = 198 (children)
y= 70 (students)
Check
99*7+198*5+70*7=2668
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The statement of the problem is defective. With the given information, there are more than one way the total ticket sales could be $2668.
The problem with the statement of the problem is that it only tells the capacity of the theater -- it does NOT say that all seats were sold.
This leaves a problem that is more interesting than the one (answered by the other tutor) in which all the seats are sold.
x = # adult tickets
2x = # children tickets
y = # student tickets
The total ticket sales was $2668:



This is a linear Diophantine equation -- a single equation with two variables, in which the values of the variables are non-negative integers. Such a problem can have several different solutions.
A standard method for finding all the solutions is to solve the equation for one of the variables and use the fact that both variables have positive integer values to find all the solutions.


Divide both sides by 7, writing the expression on the right as quotient plus remainder:


In this equation, y, 381, and 3x are all integers; that means 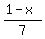 must be an integer. must be an integer.
That means the value of x can be any positive integer equal to 1 plus any multiple of 7: 1, 8, 15, 22, ....
The solutions are limited by the fact that the total number of tickets sold, 3x+y, must be less than or equal to 367.
We can make a table to find all the solutions to the problem, considering the known possible values of x.
# adults # children # students total sales # seats sold
x 2x y=381-3x+(1-x)/7 22x+7y 3x+y
-------- ---------- ---------------- ----------- ------------
1 2 378 2668 381
8 16 356 2668 380
15 30 334 2668 379
...
The expression for the total cost of the tickets is 22x+7y; this must remain at $2668. These first few entries in the table show us that, to keep the total cost constant, each time x increases by 7 y decreases by 22. These first few entries also show that each time x increases by 7 the total number of seats sold decreases by 1.
The maximum number of seats that can be sold is 367. When x=1, the total number of seats is 381, which is 14 too many. So to have no more than 367 seats sold, the minimum value of x that gives a solution to the problem is 1+14(7)=99.
We can continue the table from there to find all the solutions to the problem.
# adults # children # students total sales # seats sold
x 2x y=381-3x+(1-x)/7 22x+7y 3x+y
-------- ---------- ---------------- ----------- ------------
1 2 378 2668 381
8 16 356 2668 380
15 30 334 2668 379
...
99 198 70 2668 367
106 212 48 2668 366
113 226 26 2668 365
120 240 4 2668 364
CLearly, larger values of x will make y negative, which we can't have. So the list of solutions is complete.
We see that there are four combinations of the numbers of adult, children, and student tickets that could be sold to have a maximum of 367 tickets sold, with total ticket sales equal to $2668; the number of seats sold is between 364 and the maximum of 367.
ANSWERS:
(1) 99 adults, 198 children, 70 students (all 367 seats sold)
(2) 106 adults, 212 children, 48 students (366 seats sold)
(3) 113 adults, 226 children, 26 students (365 seats sold)
(4) 120 adults, 240 children, 4 students (364 seats sold)
Answer by ikleyn(52771)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A movie theater has a seating capacity of 367.
The theater charges $5.00 for children, $7.00 for students, and the $12.00 for adults.
There are half as many adults as there are children if the total tickets sales was $2668,
how many children, students, and adults attended?
~~~~~~~~~~~~~~~~~~~~~
It may seem amazing, but the problem can be solved using only one unknown
and one equation. I will show this solution method below.
Surely, the theater is considered to be fully filled, as it is usually
assumed in such problems, by default and from context.
Let x be the number of adults.
Then the number of children is 2x, from the problem,
and the number of students is (367-x-2x) = (367-3x).
Write the total money equation
5*(2x) + 7*(367-3x) + 12x = 2668 dollars.
Simplify this equation and find x
10x + 7*367 - 21x + 12x = 2668
10x - 21x + 12x = 2668 - 7*367
x = 99.
ANSWER. 99 adults; 2*99 = 198 children, and 367-99-198 = 70 students.
CHECK the total money: 99*12 + 198*5 + 70*7 = 2668 doll;ars. ! correct !
Solved.
---------------------
The lesson to learn: This problem seem to be solved using three (or two) unknown;
but in reality, it can be solved using one unknown and one equation,
saving your time and diminishing the number of erros.
Your task is to learn to recognize such problems from the first glance.
Answer by josgarithmetic(39615)   (Show Source): (Show Source):
You can put this solution on YOUR website! Adult quantity is half the children quantity or in other words, children quantity is twice the adult quantity.
PRICE QTY REVENUE
CHILDRN 5 2y 5*2y
STDNTS 7 367-3y 7(367-3y)
ADULTS 12 y 12y
Total 367 2668
The necessary equation is obvious.
|
|
|
| |